
题目列表(包括答案和解析)
(本小题满分12分)
某电视生产厂家有A、B两种型号的电视机参加家电下乡活动.若厂家投放A、B型号电视机的价值分别为p、q万元,农民购买电视机获得相应的补贴分别为 已知厂家把价值为10万元的A、B两种型号的电视机投放市场,且A、B两种型号的电视机投放金额都不低于1万元(精确到0.1,参考数据:
已知厂家把价值为10万元的A、B两种型号的电视机投放市场,且A、B两种型号的电视机投放金额都不低于1万元(精确到0.1,参考数据: ).
).
(1)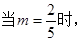 请你制定一个投放方案,使得在这次活动中农民得到的补贴最多,并求出其最大值;
请你制定一个投放方案,使得在这次活动中农民得到的补贴最多,并求出其最大值;
(2)讨论农民得到的补贴随厂家投放B型号电视机金额的变化而变化的情况.
(本小题满分12分)
在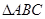 中,角A、B、C的对边分别为
中,角A、B、C的对边分别为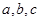 ,已知
,已知 ,且
,且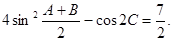
(1)求角C的大小;
(2)求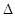 ABC的面积.
ABC的面积.
(本小题满分12分)
在△ABC中,a、b、c分别是角A、B、C的对边,且(2a+c)cosB+bcosC=0.
(Ⅰ)求角B的值;
(Ⅱ)已知函数f(x)=2cos(2x-B),将f(x)的图象向左平移 后得到函数g(x)的图象,求g(x)的单调增区间.
后得到函数g(x)的图象,求g(x)的单调增区间.
(本小题满分12分)△ABC中,内角A,B,C的对边分别为a,b,c,已知a,b,c成等比数列, .
.
(Ⅰ)求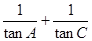 的值;
的值;
(Ⅱ)设 的值。
的值。
(本小题满分12分) 已知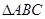 的角A、B、C所对的边分别是
的角A、B、C所对的边分别是 ,
,
设向量 ,
,  ,
, 
(Ⅰ)若 ∥
∥ ,求证:
,求证: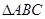 为等腰三角形;
为等腰三角形;
(Ⅱ)若 ⊥
⊥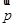 ,边长
,边长 ,
, ,求
,求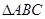 的面积.
的面积.
第Ⅰ卷(选择题,共50分)
1―3 AAD 4(文)D(理)B 5(文)B(理)C
|