
题目列表(包括答案和解析)
 ,0),N(
,0),N( ,0),动点P满足条件kPM•kPN=
,0),动点P满足条件kPM•kPN= ,记点P的轨迹为C,点R(-3,0),过点R且倾斜角为300的直线l交轨迹C于A、B两点.
,记点P的轨迹为C,点R(-3,0),过点R且倾斜角为300的直线l交轨迹C于A、B两点.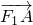 •
• ;
;



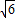 ,0),N(
,0),N(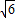 ,0),动点P满足条件kPM•kPN=
,0),动点P满足条件kPM•kPN=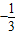 ,记点P的轨迹为C,点R(-3,0),过点R且倾斜角为30的直线l交轨迹C于A、B两点.
,记点P的轨迹为C,点R(-3,0),过点R且倾斜角为30的直线l交轨迹C于A、B两点.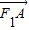 •
•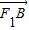 ;
;(本小题满分12分)在第9届校园文化艺术节棋类比赛项目报名过程中,我校高二(2)班共有16名男生和14名女生预报名参加,调查发现,男、女选手中分别有10人和6人会围棋.
(I)根据以上数据完成以下2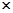 2列联表:
2列联表:
|
|
会围棋 |
不会围棋 |
总计 |
|
男 |
|
|
|
|
女 |
|
|
|
|
总计 |
|
|
30 |
并回答能否在犯错的概率不超过0.10的前提下认为性别与会围棋有关?
参考公式: 其中n=a+b+c+d
其中n=a+b+c+d
参考数据:
|
|
0.40 |
0.25 |
0.10 |
0.010 |
|
|
0.708 |
1.323 |
2.706 |
6.635 |
(Ⅱ)若从会围棋的选手中随机抽取3人成立该班围棋代表队,则该代表队中既有男又
有女的概率是多少?
(Ⅲ)若从14名女棋手中随机抽取2人参加棋类比赛,记会围棋的人数为 ,求
,求 的期望.
的期望.
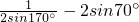 =________;
=________;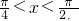 则函数y=tan2xtan3x的最大值为________;
则函数y=tan2xtan3x的最大值为________; )cos(x+
)cos(x+ )+2
)+2 cos2(x+
cos2(x+ )-
)- ,若0≤θ≤π,使函数f(x)为偶函数的θ为________
,若0≤θ≤π,使函数f(x)为偶函数的θ为________ B、
B、 C、
C、 D、
D、 .
.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com