
题目列表(包括答案和解析)
直线![]()
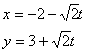 上与点P(-2,3)距离为
上与点P(-2,3)距离为![]() 的点的坐标为 .
的点的坐标为 .
 (t为参数)上与点P(-2,3)的距离等于
(t为参数)上与点P(-2,3)的距离等于 的点的坐标是
的点的坐标是| A.(-4,5) | B.(-3,4) |
| C.(-3,4)或(-1,2) | D.(-4,5)或(0,1) |
直线
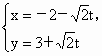 (t为参数)上与点P(-2,3)的距离等于
(t为参数)上与点P(-2,3)的距离等于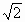 的点的坐标是
的点的坐标是
[
]A
.(-4,5)B
.(-3,4)C
.(-3,4)或(-1,2)D
.(-4,5)或(0,1)如图四棱锥P-ABCD的底面是边长为2的菱形,且∠BAD=60°,PA⊥平面ABCD,设E为BC的中点,二面角P-DE-A为45°.
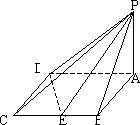
(1)求点A到平面PDE的距离;
(2)在PA上确定一点F,使BF∥平面PDE;
(3)求异面直线PC与DE所成的角(用反三角函数表示);
(4)求面PDE与面PAB所成的不大于直二面角的二面角的大小(用反三角函数表示).
如图四棱锥P-ABCD的底面是边长为2的菱形,且∠BAD=60°,PA⊥平面ABCD,设E为BC的中点,二面角P-DE-A为45°.
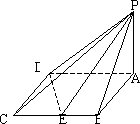
(1)求点A到平面PDE的距离;
(2)在PA上确定一点F,使BF∥平面PDE;
(3)求异面直线PC与DE所成的角(用反三角函数表示);
(4)求面PDE与面PAB所成的不大于直二面角的二面角的大小(用反三角函数表示).
一、填空题
1. 2.
2. 3.既不充分条件又不必要条件 4.[-4,-π]
3.既不充分条件又不必要条件 4.[-4,-π] [0,π]
[0,π]
5. 6.6 7.
6.6 7. 8.2个 9.等腰直角三角形
8.2个 9.等腰直角三角形
10. 11.(-3,4),(-1,2)
12.①、②、⑤
13.
11.(-3,4),(-1,2)
12.①、②、⑤
13.
14.C
二、解答题
15.(本小题满分14分)
解:(1)设 由
由 得
得
它的解集为(1,3)得方程 的两根为1和3且a<0
的两根为1和3且a<0
 即
即 ……(1)
……3分
……(1)
……3分
 有等根得
有等根得
 ……(2)
……6分
……(2)
……6分
由(1)(2)及 得
得
故 的解析式为
的解析式为 ……8分
……8分
(2)由
及 ……10分
……10分
由 ……12分
……12分
解得  ……14分
……14分
16.(本小题满分14分)
解:由 得
得 ,
………………………………2分
,
………………………………2分
又

 , ……………………………………6分
, ……………………………………6分
由 得
得 , …………………………10分
, …………………………10分
 .
……14分
.
……14分
17.(本小题满分15分).
已知二次函数 的二次项系数为
的二次项系数为 ,且不等式
,且不等式 的解集为
的解集为 .
.
(1)若方程 有两个相等的根,求
有两个相等的根,求 的解析式;
的解析式;
(2)若 的最大值为正数,求
的最大值为正数,求 的取值范围.
的取值范围.
解:(1)设 由
由 得
得
它的解集为(1,3)得方程 的两根为1和3且a<0
的两根为1和3且a<0
 即
即 ……(1)
……3分
……(1)
……3分
 有等根得
有等根得
 ……(2)
……6分
……(2)
……6分
由(1)(2)及 得
得
故 的解析式为
的解析式为 ……8分
……8分
(2)由
及 ……10分
……10分
由 ……12分
……12分
解得  ……15分
……15分
18解:(1)当m=2时,A=(-2,2),B=(-1,3)∴ A B=(-1,2).……5分
B=(-1,2).……5分
(2)当m<0时,B=(1+m,1-m)
要使B A,必须
A,必须 ,此时
,此时 m
m
当m=0时,B= ,B
,B A;适合
……10分
A;适合
……10分
当m>0时,B=(1-m,m+1)
要使B A,必须
A,必须 ,此时0<m≤1. ……13分
,此时0<m≤1. ……13分
∴综上可知,使B A的实数m的取值范围为[-1,1] ……15分
A的实数m的取值范围为[-1,1] ……15分
法2
要使B A,必须
A,必须 ,此时
,此时 m
m 1; ……13分
1; ……13分
∴使B A的实数m的取值范围为[-1,1] ……15分
A的实数m的取值范围为[-1,1] ……15分
18.(本小题满分15分)
(1)解:由 得
得 ,
,
 . ………………2分
. ………………2分
设
= <0(讨论a>1和0<a<1),
<0(讨论a>1和0<a<1),
得f(x)为R上的增函数. ………………5分
(2)由 , …………7分
, …………7分
即 得
得 , ………………9分
, ………………9分
得1<m< .
………………10分
.
………………10分
(3)f(x)在R上为增函数)f(x) 当 时)f(x)-4的值恒为负数, ………13分
时)f(x)-4的值恒为负数, ………13分
而f(x)在R上单调递增得f(2)-4 0,
………………15分
0,
………………15分
19.(本小题满分16分)
解:(1)∵f(x+1)为偶函数,
∴
 恒成立,
恒成立,
即(
∴ .
.
∵函数f(x)的图象与直线y=x相切,
∴二次方程 有两相等实数根,
有两相等实数根,
∴
 ………………6分
………………6分
(2)

 ………………8分
………………8分

即 为方程
为方程 的两根
的两根
 .
………………11分
.
………………11分
∵m<n且 .
.
故当 ;
;
当k>1时,
当k=1时,[m,n]不存在. ………………16分
20.(本小题满分16分)
解:(1)若 为函数f(x)不动点,则有
为函数f(x)不动点,则有 ,
,
整理得  ①
………………2分
①
………………2分
根据题意可判断方程①有两个根,且这两个根互为相反数,得
 >
> ,
, <0
<0
所以b=3 ,a>0 ………………4分
而 ,所以
,所以 .
.
即b=3,a>0,且a≠9. ………………5分
(2)在(1)的条件下,当a=8时, .
.
由 ,解得两个不动点为
,解得两个不动点为 ,……6分
,……6分
设点P(x ,y),则y>3 ,即 >3解得x<-3 .
………………8分
>3解得x<-3 .
………………8分
设点P(x,y)到直线A

 .
………………10分
.
………………10分
当且仅当 ,即x=―4时,取等号,此时P(―4,4). ……12分
,即x=―4时,取等号,此时P(―4,4). ……12分
(3)命题正确. ………………13分
因为f(x)定义在R上的奇函数,所以f(―0)=―f(0) ,所以0是奇函数f(x)的一个不动点.
设c≠0是奇函数f(x)的一个不动点,则f(c)=c
,由 ,所以―c也是f (x)的一个不动点.
,所以―c也是f (x)的一个不动点.
所以奇函数f(x)的非零不动点如果存在,则必成对出现,故奇函数f(x)的不动点数目是奇数个. ………………16分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com