
题目列表(包括答案和解析)
 选做题在A、B、C、D四小题中只能选做2题,每小题10分,共计20分.
选做题在A、B、C、D四小题中只能选做2题,每小题10分,共计20分.| 1 |
| 3 |
|
| β |
|
| a |
| a |
| β |
| a |
| 3cos2θ+4sin2θ |
| (a+b+c)2 |
| 3 |
 [选做题]在A、B、C、D四小题中只能选做2题,每小题10分,计20分.请把答案写在答题纸的指定区域内.
[选做题]在A、B、C、D四小题中只能选做2题,每小题10分,计20分.请把答案写在答题纸的指定区域内.
|
|
| π |
| 2 |
| π |
| 4 |
| a2+b2 |
| c2+d2 |
| (ac+bd)(ad+bc) |
 [选做题]在A、B、C、D四小题中只能选做2题,每小题10分,计20分.请把答案写在答题纸的指定区域内.
[选做题]在A、B、C、D四小题中只能选做2题,每小题10分,计20分.请把答案写在答题纸的指定区域内.
|
|
| π |
| 4 |
| 2 |
| c |
| 4 |
| c |
| 6 |
 选做题在A、B、C、D四小题中只能选做2题,每小题10分,共计20分.
选做题在A、B、C、D四小题中只能选做2题,每小题10分,共计20分.
|
|
|
| 1 |
| b |
| 1 |
| 2a |
[选做题]在A、B、C、D四小题中只能选做两题,每小题10分,共计20分。请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤。
A.选修4 - 1:几何证明选讲
如图,在四边形ABCD中,△ABC≌△BAD。

求证:AB∥CD。
B.选修4 - 2:矩阵与变换
求矩阵![]() 的逆矩阵。
的逆矩阵。
C.选修4 - 4:坐标系与参数方程
已知曲线C的参数方程为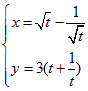 (
(![]() 为参数,
为参数,![]() ),求曲线C的普通方程。
),求曲线C的普通方程。
D.选修4 - 5:不等式选讲
设![]() ≥
≥![]() >0,求证:
>0,求证:![]() ≥
≥![]() 。
。
一、填空题:本大题共14小题,每小题5分,计70分.
1.  2.
2.  3.
3. 4.
4.  5.68 6. 4 7. 7 8.
5.68 6. 4 7. 7 8. 
9. 10. 若点P在两渐近线上的射影分别为
10. 若点P在两渐近线上的射影分别为 、
、 ,则
,则 必为定值
必为定值
11.②③
12. 13.1 14.
13.1 14.
二、解答题:本大题共6小题,计90分.
15. 解: (Ⅰ)因为 ,∴
,∴ ,则
,则 …………………………………………(4分)
…………………………………………(4分)
∴ ……………………………………………………………………………(7分)
……………………………………………………………………………(7分)
(Ⅱ)由 ,得
,得 ,∴
,∴ …………………………………………(9分)
…………………………………………(9分)
则 …………………………………………(11分)
…………………………………………(11分)
由正弦定理,得 ,∴
,∴ 的面积为
的面积为 ………………………(14分)
………………………(14分)
16. (Ⅰ)解:因为 ,
, ,且
,且 ,
,
所以 ……………………………………………………………………………………………(4分)
……………………………………………………………………………………………(4分)
又 ,所以四边形
,所以四边形 为平行四边形,则
为平行四边形,则 ……………………………………(6分)
……………………………………(6分)
而 ,故点
,故点 的位置满足
的位置满足 ………………………………………………………(7分)
………………………………………………………(7分)
(Ⅱ)证: 因为侧面 底面
底面 ,
, ,且
,且 ,
,
所以 ,则
,则 …………………………………………………………………(10分)
…………………………………………………………………(10分)
又 ,且
,且 ,所以
,所以 …………(13分)
…………(13分)
而 ,所以
,所以 …………………………………………………(14分)
…………………………………………………(14分)
17. 解:(Ⅰ)因为 ,所以
,所以 的面积为
的面积为 (
( )………………………(2分)
)………………………(2分)
设正方形 的边长为
的边长为 ,则由
,则由 ,得
,得 ,
,
解得 ,则
,则 …………………………………………………………………(6分)
…………………………………………………………………(6分)
所以 ,则
,则 ………………(9分)
………………(9分)
(Ⅱ)因为 ,所以
,所以
 ……………(13分)
……………(13分)
当且仅当 时取等号,此时
时取等号,此时 .所以当
.所以当 长为
长为 时,
时, 有最小值1…………………(15分)
有最小值1…………………(15分)
18. 解:(Ⅰ)设圆心
 ,则
,则 ,解得
,解得 …………………………………(3分)
…………………………………(3分)
则圆 的方程为
的方程为 ,将点
,将点 的坐标代入得
的坐标代入得 ,故圆
,故圆 的方程为
的方程为 ………(5分)
………(5分)
(Ⅱ)设 ,则
,则 ,且
,且 …………………………(7分)
…………………………(7分)
= =
= ,所以
,所以 的最小值为
的最小值为 (可由线性规划或三角代换求得)…(10分)
(可由线性规划或三角代换求得)…(10分)
(Ⅲ)由题意知, 直线 和直线
和直线 的斜率存在,且互为相反数,故可设
的斜率存在,且互为相反数,故可设 ,
,
 ,由
,由 ,得
,得 ………(11分)
………(11分)
因为点 的横坐标
的横坐标 一定是该方程的解,故可得
一定是该方程的解,故可得 ………………………………(13分)
………………………………(13分)
同理, ,所以
,所以 =
=
所以,直线 和
和 一定平行…………………………………………………………………………(15分)
一定平行…………………………………………………………………………(15分)
19. (Ⅰ)解:因为 …………………………………(2分)
…………………………………(2分)
由 ;由
;由 ,所以
,所以 在
在 上递增,
上递增,
在 上递减 …………………………………………………………………………………………(4分)
上递减 …………………………………………………………………………………………(4分)
欲 在
在 上为单调函数,则
上为单调函数,则 ………………………………………………………(5分)
………………………………………………………(5分)
(Ⅱ)证:因为 在
在 上递增,在
上递增,在 上递减,所以
上递减,所以 在
在 处取得极小值
处取得极小值 (7分)
(7分)
又 ,所以
,所以 在
在 上的最小值为
上的最小值为 …………………………………(9分)
…………………………………(9分)
从而当 时,
时, ,即
,即 …………………………………………………………(10分)
…………………………………………………………(10分)
(Ⅲ)证:因为 ,所以
,所以 即为
即为 ,
,
令 ,从而问题转化为证明方程
,从而问题转化为证明方程 =0
=0
在 上有解,并讨论解的个数……………………………………………………………………(12分)
上有解,并讨论解的个数……………………………………………………………………(12分)
因为 ,
, ,所以
,所以
①当 时,
时, ,所以
,所以 在
在 上有解,且只有一解 ……(13分)
上有解,且只有一解 ……(13分)
②当 时,
时, ,但由于
,但由于 ,
,
所以 在
在 上有解,且有两解 …………………………………………………………(14分)
上有解,且有两解 …………………………………………………………(14分)
③当 时,
时, ,所以
,所以 在
在 上有且只有一解;
上有且只有一解;
当 时,
时, ,
,
所以 在
在 上也有且只有一解…………………………………………………………(15分)
上也有且只有一解…………………………………………………………(15分)
综上所述, 对于任意的 ,总存在
,总存在 ,满足
,满足 ,
,
且当 时,有唯一的
时,有唯一的 适合题意;当
适合题意;当 时,有两个
时,有两个 适合题意…………(16分)
适合题意…………(16分)
(说明:第(Ⅱ)题也可以令 ,
, ,然后分情况证明
,然后分情况证明 在其值域内,并讨论直线
在其值域内,并讨论直线 与函数
与函数 的图象的交点个数即可得到相应的
的图象的交点个数即可得到相应的 的个数)
的个数)
20.(Ⅰ)解:由题意得, ,所以
,所以 =
= ……………………(4分)
……………………(4分)
(Ⅱ)证:令 ,
, ,则
,则 =1………………………………………………(5分)
=1………………………………………………(5分)
所以 =
= (1),
(1), =
= (2),
(2),
(2)―(1),得 ―
― =
= ,
,
化简得 (3)……………………………………………………………(7分)
(3)……………………………………………………………(7分)
 (4),(4)―(3)得
(4),(4)―(3)得 …………(9分)
…………(9分)
在(3)中令 ,得
,得 ,从而
,从而 为等差数列 …………………………………………(10分)
为等差数列 …………………………………………(10分)
(Ⅲ)记 ,公差为
,公差为 ,则
,则 =
= …………………(12分)
…………………(12分)
则 ,
,

 …………………………………………(14分)
…………………………………………(14分)
则 ,当且仅当
,当且仅当 ,即
,即 时等号成立……………(16分)
时等号成立……………(16分)
数学附加题部分
21.A.(几何证明选讲选做题)
解:因为PB=PD+BD=1+8=9, =PD?BD=9,PA=3,AE=PA=3,连结AD,在
=PD?BD=9,PA=3,AE=PA=3,连结AD,在 中,得
中,得 ……(5分)
……(5分)
又 ,所以
,所以 …………………………………………………………………(10分)
…………………………………………………………………(10分)
B.(矩阵与变换选做题)
解: (Ⅰ)设 ,则有
,则有
 =
= ,
,
 =
= ,
,
所以 ,解得
,解得 …………………………………………………………(4分)
…………………………………………………………(4分)
所以M= ,从而
,从而 =
= ………………………………………………………………(7分)
………………………………………………………………(7分)
(Ⅱ)因为 且m:2
且m:2 ,
,
所以2(x+2y)-(3x+4y)=4,即x+4 =0,这就是直线l的方程 ………………………………………(10分)
C.(坐标系与参数方程选做题)
解:将极坐标方程 转化为普通方程:
转化为普通方程: ……………………………………………(2分)
……………………………………………(2分)
 可化为
可化为 …………………………………………………………(5分)
…………………………………………………………(5分)
在 上任取一点A
上任取一点A ,则点A到直线的距离为
,则点A到直线的距离为
 ,它的最大值为4
……………………………(10分)
,它的最大值为4
……………………………(10分)
D.(不等式选讲选做题)
证:左=
 …(5分)
…(5分)

 ……………………(10分)
……………………(10分)
22.解:以OA、OB所在直线分别x轴,y轴,以过O且垂直平面ABCD的直线为z轴,建立空间直角坐标系,则 ,
, …(2分)
…(2分)
(Ⅰ)设平面PDB的法向量为 ,
,
由 ,
,
所以 =
= …………………………………………………(5分)
…………………………………………………(5分)
(Ⅱ)设平面ABP的法向量 ,
, ,
,
 ,
, ,
,
 ,而所求的二面角与
,而所求的二面角与 互补,
互补,
所以二面角A―PB―D的余弦值为 …………………………………………………………………(10分)
…………………………………………………………………(10分)
23.解:(Ⅰ)设袋中原有n个白球,由题意知: ,所以
,所以 =12,
=12,
解得n=4(舍去 ),即袋中原有4个白球……………………………………………………………(3分)
),即袋中原有4个白球……………………………………………………………(3分)
(Ⅱ)由题意, 的可能取值为1,2,3,4………………………………………………………………(4分)
的可能取值为1,2,3,4………………………………………………………………(4分)
 ,
,
所以,取球次数 的分布列为:
的分布列为:

1
2
3
4
P




………(6分)
 …………………………………………………………………………………………………(8分)
…………………………………………………………………………………………………(8分)
(Ⅲ)因为甲先取,所以甲只有可能在第1次和第3次取球,记“甲取到白球”的事件为A,
则 或 “
或 “ =3”),所以
=3”),所以 ………………………(10分)
………………………(10分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com