
题目列表(包括答案和解析)
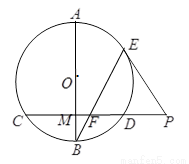
如图,已知⊙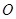 中,直径
中,直径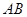 垂直于弦
垂直于弦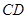 ,垂足为
,垂足为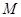 ,
,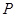 是
是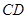 延长线上一点,
延长线上一点,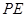 切⊙
切⊙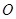 于点
于点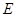 ,连接
,连接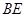 交
交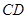 于点
于点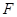 ,证明:
,证明: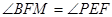
【解析】本试题主要考查了直线与圆的位置关系的运用。要证明角相等,一般运用相似三角形来得到,或者借助于弦切角定理等等。根据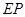 为⊙
为⊙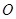 的切线,∴
的切线,∴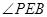 为弦切角
为弦切角
连接 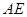 ∴
∴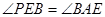 …注意到
…注意到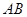 是直径且垂直弦
是直径且垂直弦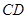 ,所以
,所以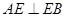 且
且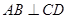 …利用
…利用 ,可以证明。
,可以证明。
解:∵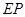 为⊙
为⊙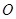 的切线,∴
的切线,∴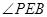 为弦切角
为弦切角
连接 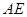 ∴
∴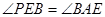 ……………………4分
……………………4分
又∵ 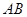 是直径且垂直弦
是直径且垂直弦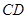 ∴
∴ 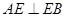 且
且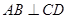 ……………………8分
……………………8分
∴  ∴
∴ 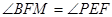
(本小题满分12分)一名高二学生盼望进入某名牌大学学习,不放弃能考入该大学的任何一次机会。已知该大学通过以下任何一种方式都可被录取:
① 2010年2月国家数学奥赛集训队考试通过(集训队从2009年10月省数学竞赛壹等奖获得者中选拔,通过考试进入集训队则能被该大学提前录取);
② 2010年3月自主招生考试通过并且2010年6月高考分数达重点线;
③ 2010年6月高考达到该校录取分数线(该校录取分数线高于重点线)。
该名考生竞赛获省一等奖、自主招生考试通过、高考达重点线、高考达该校分数线等事件的概率如下表:
| 事件 | 省数学竞获一等奖 | 自主招生考试通过 | 高考达重点线 | 高考达该校分数线 |
| 概率 | 0.5 | 0.7 | 0.8 | 0.6 |
如果数学竞赛获省一等奖,该学生估计自己进入国家集训队的概率是0.4。
(1)求该学生参加自主招生考试的概率;
(2)求该学生参加考试次数的分布列与数学期望;
(3)求该学生被该大学录取的概率。
(本小题满分12分)一名高二学生盼望进入某名牌大学学习,不放弃能考入该大学的任何一次机会。已知该大学通过以下任何一种方式都可被录取:
① 2010年2月国家数学奥赛集训队考试通过(集训队从2009年10月省数学竞赛壹等奖获得者中选拔,通过考试进入集训队则能被该大学提前录取);
② 2010年3月自主招生考试通过并且2010年6月高考分数达重点线;
③ 2010年6月高考达到该校录取分数线(该校录取分数线高于重点线)。
该名考生竞赛获省一等奖、自主招生考试通过、高考达重点线、高考达该校分数线等事件的概率如下表:
| 事件 | 省数学竞获一等奖 | 自主招生考试通过 | 高考达重点线 | 高考达该校分数线 |
| 概率 | 0.5 | 0.7 | 0.8 | 0.6 |
如果数学竞赛获省一等奖,该学生估计自己进入国家集训队的概率是0.4。
(1)求该学生参加自主招生考试的概率;
(2)求该学生参加考试次数的分布列与数学期望;
(3)求该学生被该大学录取的概率。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com