
题目列表(包括答案和解析)
| 温度x/℃ | 21 | 23 | 25 | 27 | 29 | 32 | 35 |
| 产卵数y/个 | 7 | 11 | 21 | 24 | 66 | 115 | 325 |
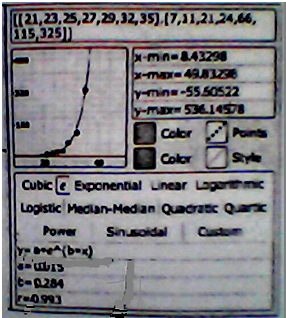
| ① | ② | ③ | ④ | ||||||||||||||||||||||||||
| 模型 | y=ax+b | y=aebx | y=ax2+c | y=ax3+bx2+cx+d | |||||||||||||||||||||||||
| 计算结果 |
|
|
|
|
(本题满分15分)抛物线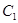 的方程是
的方程是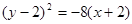 ,曲线
,曲线 与
与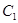 关于点
关于点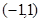 对称.(Ⅰ)求曲线
对称.(Ⅰ)求曲线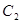 的方程;
(Ⅱ)过点(8,0)的直线
的方程;
(Ⅱ)过点(8,0)的直线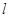 交曲线
交曲线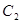 于M、N两点,问在坐标平面上能否找到某个定点
于M、N两点,问在坐标平面上能否找到某个定点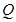 ,不论直线
,不论直线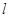 如何变化,总有
如何变化,总有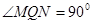 。若找不到,请说明理由;若能找到,写出满足要求的所有的点
。若找不到,请说明理由;若能找到,写出满足要求的所有的点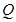 的坐标.
的坐标.
若x1、x2是关于一元二次方程ax2+bx+c(a≠0)的两个根,则方程的两个根x1、x2和系数a、b、c有如下关系:x1+x2=- ,x1•x2=
,x1•x2= .把它称为一元二次方程根与系数关系定理.如果设二次函数y=ax2+bx+c(a≠0)的图象与x轴的两个交点为A(x1,0),B(x2,0).利用根与系数关系定理可以得到A、B连个交点间的距离为:
.把它称为一元二次方程根与系数关系定理.如果设二次函数y=ax2+bx+c(a≠0)的图象与x轴的两个交点为A(x1,0),B(x2,0).利用根与系数关系定理可以得到A、B连个交点间的距离为:
AB=|x1-x2|= =
= =
= =
= .
.

参考以上定理和结论,解答下列问题:
设二次函数y=ax2+bx+c(a>0)的图象与x轴的两个交点A(x1,0)、B(x2,0),抛物线的顶点为C,显然△ABC为等腰三角形.
(1)当△ABC为直角三角形时,求b2-4ac的值;
(2)当△ABC为等边三角形时,求b2-4ac的值.
 ,x1•x2=
,x1•x2= .把它称为一元二次方程根与系数关系定理.如果设二次函数y=ax2+bx+c(a≠0)的图象与x轴的两个交点为A(x1,0),B(x2,0).利用根与系数关系定理可以得到A、B连个交点间的距离为:
.把它称为一元二次方程根与系数关系定理.如果设二次函数y=ax2+bx+c(a≠0)的图象与x轴的两个交点为A(x1,0),B(x2,0).利用根与系数关系定理可以得到A、B连个交点间的距离为: =
= =
= =
= .
.
(本题满分18分)本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分8分.
已知点是直角坐标平面内的动点,点到直线的距离为,到点的距离为,且.
(1)求动点P所在曲线C的方程;
(2)直线过点F且与曲线C交于不同两点A、B(点A或B不在x轴上),分别过A、B点作直线的垂线,对应的垂足分别为,试判断点F与以线段为直径的圆的位置关系(指在圆内、圆上、圆外等情况);
(3)记,,(A、B、是(2)中的点),问是否存在实数,使成立.若存在,求出的值;若不存在,请说明理由.
进一步思考问题:若上述问题中直线、点、曲线C:,则使等式成立的的值仍保持不变.请给出你的判断 (填写“不正确”或“正确”)(限于时间,这里不需要举反例,或证明).
1.B 提示:在同一坐标系中画出两函数y = a |x|与y = |log a x|图象,如图

2.D提示: 如图|OM| = 2,|AM| = ,|OA| = 1,∴k = tan∠AOM = 。

3.B提示:
A=[0,4],B=[-4,0],
4.D
5.B 提示:如图

6.C 提示:
 而|z|表示
而|z|表示

7.A 提示:T=2×8=16,则 ,令
,令 。
。
8.A 提示:在同一坐标系中作出函数 的图象,易得。
的图象,易得。

9.A 提示:在同一坐标系中画出函数y=4x+1,y=x+2和y=-2x+4的图象,由图可知,f(x)的最高点为 。
。
10.D 提示:由可行域易知z=5x+y过点(1,0)时取得最大值5.
11.B 提示: f(x)= f(-x)= f(2-x),故f(x)的草图如图:

由图可知,B正确。
12.C提示:设椭圆另一焦点为F2,(如图), ,又注意到N、O各为MF1、F1F2的中点,
∴ON是△MF1F2的中位线,
,又注意到N、O各为MF1、F1F2的中点,
∴ON是△MF1F2的中位线, 

13.f (1) < f (4) < f (- 3)提示:由f (2 + t) = f (2 ? t)知,f(x)的图象关于直线x=2对称,又f (x) = x 2 + bx + c为二次函数,其图象是开口向上的抛物线,由f(x)的图象,易知f (1) < f (4) < f (- 3).
14.1 < m < 5提示:设y 1 = x 2 ? 4|x| + 5,y 2 = m,画出两函数图象示意图,要使方程x 2 ? 4|x| + 5 = m有四个不相等实根,只需使1 < m < 5.

15.
提示:y=x-m表示倾角为45°,纵截距为-m的直线方程,而 则表示以(0,0)为圆心,以1为半径的圆在x轴上方的部分(包括圆与x轴的交点),如下图所示,显然,欲使直线与半圆有两个不同交点,只需直线的纵截距
则表示以(0,0)为圆心,以1为半径的圆在x轴上方的部分(包括圆与x轴的交点),如下图所示,显然,欲使直线与半圆有两个不同交点,只需直线的纵截距 ,即
,即 .
.

16、


 ,
,

九、实战演习
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 方程 的实根的个数为( )
的实根的个数为( )
A. 1个 B. 2个 C. 3个 D. 4个
2. 函数 的图象恰有两个公共点,则实数a的取值范围是( )
的图象恰有两个公共点,则实数a的取值范围是( )
A.  B.
B.

C.  D.
D.

3. 若不等式 的解集为
的解集为 则a的值为( )
则a的值为( )
A. 1 B. 2 C. 3 D. 4
4. 若 时,不等式
时,不等式 恒成立,则a的取值范围为( )
恒成立,则a的取值范围为( )
A. (0,1) B. (1,2) C. (1,2] D. [1,2]
5 已知f(x)=(x?a)(x?b)?2(其中a<b
已知f(x)=(x?a)(x?b)?2(其中a<b ,且α、β是方程f(x)=0的两根(α<β
,且α、β是方程f(x)=0的两根(α<β ,则实数a、b、α、β的大小关系为( )
,则实数a、b、α、β的大小关系为( )
6.已知x+y+1=0,则 的最小值是( )
的最小值是( )
A. B.
B. C.
C. D.
D. .
.
7.如图,是周期为 的三角函数y=f(x)的图像,那么f(x)可以写成( )
的三角函数y=f(x)的图像,那么f(x)可以写成( )

A.sin(1+x) B.sin(-1-x) C.sin(x-1) D.sin(1-x)
8.方程x+log3x=2,x+log2x=2的根分别是α、β,那么α与β的大小关系是( )
A.α>β B.α<β C.α=β D.不确定.
9.

10. 在约束条件 下,当
下,当 时,目标函数
时,目标函数 的最大值的变化范围是( )
的最大值的变化范围是( )
A.  B.
B.
 C.
C.  D.
D.

11. 若不等式 在(0,
在(0, )内恒成立,则a的取值范围( )
)内恒成立,则a的取值范围( )
A.[  ,1)
B.(
,1)
B.(  ,1) C.(0,
,1) C.(0,  )
D.(0,
)
D.(0,  ]
]
12.已知 ,关于x的方程
,关于x的方程 有两个不同的实数解,则实数a的取值范围是( )
有两个不同的实数解,则实数a的取值范围是( )
A.[-2,2] B.[ ,2]
C.(
,2]
C.(  ,2] D.(
,2] D.(  ,2)
,2)
二、填空题:本大题共4小题,每小题4分,共16分,请把答案直接填在题中横线上.
13.曲线y=1+ (?2≤x≤2)与直线y=r(x?2)+4有两个交点时,实数r的取值范围___________.
(?2≤x≤2)与直线y=r(x?2)+4有两个交点时,实数r的取值范围___________.
14
. 若关于x的方程 有四个不相等的实根,则实数m的取值范围为___________。
有四个不相等的实根,则实数m的取值范围为___________。
15. 函数 的最小值为___________。
的最小值为___________。
16. 对于每个实数x,设f(x)是4x+1,x+2和-2x+4三者中的最小者,则f(x)的最大值为_________.
三、解答题:本大题共6小题,共74分,解答应写出必要的文字说明、证明过程或演算步骤.
17. (12分)若不等式 的解集为A,且
的解集为A,且 ,求a的取值范围。
,求a的取值范围。
18.(12分)设 ,试求
,试求 方程有解时k的取值范围。
方程有解时k的取值范围。
19 (12分)已知圆C:(x+2)2+y2=1,点P(x,y)为圆C上任一点.
(12分)已知圆C:(x+2)2+y2=1,点P(x,y)为圆C上任一点.
⑴求 的最值. ⑵求x-2y的最值.
的最值. ⑵求x-2y的最值.
20. (12分)设A={(x,y)|y= ,a>0},B={(x,y)|(x?1)2+(y?
,a>0},B={(x,y)|(x?1)2+(y? )2=a2,a>0},且A∩B≠
)2=a2,a>0},且A∩B≠ ,求a的最大值与最小值
,求a的最大值与最小值
21. (12分)设f(x)= ,a,b∈R,且a≠b.求证:|f(a)-f(b)|<|a-b|.
,a,b∈R,且a≠b.求证:|f(a)-f(b)|<|a-b|.
22 (12分)已知A(1,1)为椭圆
(12分)已知A(1,1)为椭圆 =1内一点,F1为椭圆左焦点,P为椭圆上一动点
=1内一点,F1为椭圆左焦点,P为椭圆上一动点 求|PF1|+|PA|的最大值和最小值
求|PF1|+|PA|的最大值和最小值
参考答案:
一、选择题
1. C 解析:画出 在同一坐标系中的图象,即可。
在同一坐标系中的图象,即可。

2. D 解析:画出 的图象
的图象


情形1: 情形2:
情形2:
3. B 解析:画出 的图象,依题意,
的图象,依题意, 从而
从而 。
。

4. C 解析:令 ,画出两函数图象.
,画出两函数图象.


a>1

若a>1,当 时,要使
时,要使 ,只需使
,只需使 ,∴
,∴ ;
;
若 ,显然当
,显然当 时,不等式
时,不等式 恒不成立。
恒不成立。
5 A
解析
A
解析 a,b是方程g(x)=(x?a)(x?b)=0的两根,在同一坐标系中作出函数f(x)、g(x)的图象如图所示
a,b是方程g(x)=(x?a)(x?b)=0的两根,在同一坐标系中作出函数f(x)、g(x)的图象如图所示

6. B 解析:方程x+y+1=0表示直线,而式子 表示点(1,1)到直线上点的距离,因此式子的最小值就是点(1,1)到直线x+y+1=0的距离,由点到直线的距离公式可求.
表示点(1,1)到直线上点的距离,因此式子的最小值就是点(1,1)到直线x+y+1=0的距离,由点到直线的距离公式可求.
7. D 解析:由周期为 得,ω=1,令1×1+φ=
得,ω=1,令1×1+φ= 得, φ=
得, φ= -1.所以y=sin(x+
-1.所以y=sin(x+ -1)=-sin(x-1)=sin(1-x).
-1)=-sin(x-1)=sin(1-x).
8. A 解析:由题意有, log3x=2-x, log2x=2-x,在同一坐标系中作出y=log3x,y=log2x,y=2-x的图像,

易见α>β.
9. D 解析:k=tan60°= .
.


(9题图) (10题图)
10. 解析:画出可行域如图
∵ ,∴在图中A点和B点处,目标函数z分别取得最大值的最小和最大.
,∴在图中A点和B点处,目标函数z分别取得最大值的最小和最大.
∴zmax∈[7,8].故选D.
11. 解析:不等式变形为 ,令y1=x2,y2=logax,如图
,令y1=x2,y2=logax,如图
函数y2过点A( )时,a=
)时,a= ,为满足条件的a边界,故a的范围是
,为满足条件的a边界,故a的范围是 ≤a<1.
≤a<1.


(11题图) (12题图)
12.D. 解析:在坐标系中画出y= 的图象.
的图象.
二、填空题
13. ( ] 解析
] 解析 方程y=1+
方程y=1+ 的曲线为半圆,y=r(x?2)+4为过(2,4)的直线. 14.
的曲线为半圆,y=r(x?2)+4为过(2,4)的直线. 14.  解析:设
解析:设 ,
,
画出两函数图象示意图,要使方程 有四个不相等实根,只需使
有四个不相等实根,只需使 .
.

15. 解析:对 ,它表示点(x,1)到(1,0)的距离;
,它表示点(x,1)到(1,0)的距离; 表示点(x,1)到点(3,3)的距离,于是
表示点(x,1)到点(3,3)的距离,于是 表示动点(x,1)到两个定点(1,0)、(3,3)的距离之和,结合图形,易得
表示动点(x,1)到两个定点(1,0)、(3,3)的距离之和,结合图形,易得 。
。
16. 解析:在同一坐标系中画出三个函数的图像,如图, 由图知, f(x)的最高点为A( ),
),

所以, f(x)的最大值为 .
.
三、解答题
17. 解:令 表示以(2,0)为圆心,以2为半径的圆在x轴的上方的部分(包括圆与x轴的交点),如下图所示,
表示以(2,0)为圆心,以2为半径的圆在x轴的上方的部分(包括圆与x轴的交点),如下图所示, 表示过原点的直线系,不等式
表示过原点的直线系,不等式 的解,即是两函数图象中半圆在直线上方的部分所对应的x值。
的解,即是两函数图象中半圆在直线上方的部分所对应的x值。
由于不等式解集 , 因此,只需要
, 因此,只需要
∴a的取值范围为(2,+ )。
)。


(17题图) (18题图)
18. 解:将原方程化为: ,
,
∴
令 ,它表示倾角为45°的直线系,
,它表示倾角为45°的直线系, ;
;
令 ,它表示焦点在x轴上,顶点为(-a,0)(a,0)的等轴双曲线在x轴上方的部分,
,它表示焦点在x轴上,顶点为(-a,0)(a,0)的等轴双曲线在x轴上方的部分,
原方程有解,则两个函数的图象有交点,由图知 ,
,
∴ . ∴k的取值范围为
. ∴k的取值范围为


(1) (2)
(1)设Q(1,2),则 的最值分别为过Q点的圆C的两条切线的斜率.如图
的最值分别为过Q点的圆C的两条切线的斜率.如图
设PQ:y-2=k(x-1),即kx-y+2-k=0
∴ ,∴k=
,∴k= 或k=
或k= .
.
∴ 的最大值为
的最大值为 ,最小值为
,最小值为 .
.
(2)令x-2y=b,即x-2y―b=0,为一组平行直线系,则x-2y=b的最值就是直线与圆相切时.如图
由 得,b=-2+
得,b=-2+ ,或b=-2-
,或b=-2- .
.
∴x-2y的最大值为-2+ ,最小值为-2-
,最小值为-2- .
.
20.解 ∵集合A中的元素构成的图形是以原点O为圆心,
∵集合A中的元素构成的图形是以原点O为圆心, a为半径的半圆;集合B中的元素是以点O′(1,
a为半径的半圆;集合B中的元素是以点O′(1, )为圆心,a为半径的圆
)为圆心,a为半径的圆 如图所示
如图所示

∴当半圆O和圆O′外切时,a最小.∴ a+a=|OO′|=2,∴amin=2
a+a=|OO′|=2,∴amin=2 ?2
?2
当半圆O与圆O′内切时, a最大 ∴
∴ a?a=|OO′|=2,∴amax=2
a?a=|OO′|=2,∴amax=2 +2
+2
21.解:由y= 得,y2-x2=1(y>x),表示的曲线为双曲线的上支,且此双曲线的渐近线为y=±x.
得,y2-x2=1(y>x),表示的曲线为双曲线的上支,且此双曲线的渐近线为y=±x.
在曲线上任取两点A(a,f(a)),A(b,f(b)),其斜率为k,由双曲线性质得|k|<1.
∴ ,∴|f(a)-f(b)|<|a-b|.
,∴|f(a)-f(b)|<|a-b|.


(21题图) (22题图)
22 解 由
由 可知a=3,b=
可知a=3,b= ,c=2,左焦点F1(?2,0),右焦点F2(2,0)
,c=2,左焦点F1(?2,0),右焦点F2(2,0)
如图 由椭圆定义,|PF1|=2a?|PF2|=6?|PF2|,
由椭圆定义,|PF1|=2a?|PF2|=6?|PF2|,
∴|PF1|+|PA|=6?|PF2|+|PA|=6+|PA|?|PF2|
由||PA|?|PF2||≤|AF2|= 知
知
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com