
题目列表(包括答案和解析)
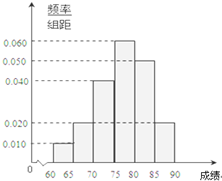
)某次考试结束后,学校从参加检测的高一学生中随机抽出60名学生,将其数学成绩(均为整数)分成六段[40,50),[50,60),…,[90,100]后得到如下部分频率分布直方图.观察图形的信息,回答下列问题:
(1)求分数在[70,80)内的频率,并补全这个频率分布直方图;
(2)统计方法中,同一组数据常用该组区间的中点值作为代表,据此估计本次考试中的平均分;

| 学生 | A1 | A2 | A3 | A4 | A5 |
| 数学 | 89 | 91 | 93 | 95 | 97 |
| 物理 | 87 | 89 | 89 | 92 | 93 |
| 学生 | 1 | 2 | 3 | 4 | 5 |
| 数学 | 89 | 91 | 93 | 95 | 97 |
| 物理 | 87 | 89 | 89 | 92 | 93 |
 在某次综合素质测试中,共设有40个考室,每个考室30名考生.在考试结束后,为调查其测试前的培训辅导情况与测试成绩的相关性,抽取每个考室中座位号为05的考生,统计了他们的成绩,得到如图所示的频率分布直方图.
在某次综合素质测试中,共设有40个考室,每个考室30名考生.在考试结束后,为调查其测试前的培训辅导情况与测试成绩的相关性,抽取每个考室中座位号为05的考生,统计了他们的成绩,得到如图所示的频率分布直方图.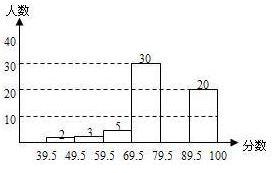 22、我市今年高三体育考试结束后,从某县3000名参考学生中抽取了100名考生成绩进行统计分析(满分100分,记分均为整数),得到如图所示的频数分布直方图,请你根据图形完成下列问题:
22、我市今年高三体育考试结束后,从某县3000名参考学生中抽取了100名考生成绩进行统计分析(满分100分,记分均为整数),得到如图所示的频数分布直方图,请你根据图形完成下列问题:一、选择题

二.填空题
(13)  (14)10;
(15)180;
(16)① ③④
(14)10;
(15)180;
(16)① ③④
三.解答题
(17)(本小题满分10分)
解 :
(Ⅰ)


 函数
函数  的单调增区间为
的单调增区间为
(Ⅱ)
(18)(本小题满分12分)
解:(I)当


(II)由(I)得 

(19)(本小题满分12分)
解:依题意,第四项指标抽检合格的概率为  其它三项指标抽检合格的概率均为
其它三项指标抽检合格的概率均为

(I)若食品监管部门对其四项质量指标依次进行严格的检测,恰好在第三项指标检测结束
时, 能确定该食品不能上市的概率等于第一、第二项指标中恰有一项不合格而且第三项指标不合格的概率.

(II)该品牌的食品能上市的概率等于四项指标都含格或第一、第二、第三项指标中仅有
一项不合格且第四项指标合格的概率.

(20)(本小题满分12分)
解法1:(I)取A

 C
C CD⊥AlCl.
CD⊥AlCl.
 底面
底面  ABC是边长为2的正三角形,
ABC是边长为2的正三角形,
 AB=BC=2,A1B1=BlCl=2,
AB=BC=2,A1B1=BlCl=2,
 B1D⊥AlCl.
B1D⊥AlCl.
又 BlD
BlD CD=D,
CD=D, A
A
(II)  面A1ACCl⊥底面ABC,
面A1ACCl⊥底面ABC, 面AlACC1⊥A1BlC1
面AlACC1⊥A1BlC1
又B1D⊥AlC1 BID⊥面A1CCl
过点D作DE⊥A
 B1ED为所求二面角的平面角
B1ED为所求二面角的平面角
又 A
A C
C


故所求二面角B1一A .
.
解法2:(I)取AC中点O,连结BO, 
 ABC是正三角形
ABC是正三角形 BO⊥AC
BO⊥AC
又面 A1ACC1⊥底面ABC, BO⊥面A1ACC1 ,
BO⊥面A1ACC1 ,  BO⊥OA1
BO⊥OA1
又AlA=A A1O⊥AC,如图建立空间直角坐标系O一xyz
A1O⊥AC,如图建立空间直角坐标系O一xyz
 则
则 (Ⅱ)
(Ⅱ) 为平面A1B
为平面A1B
. 

故二面角B1-A
(21)(本小题满分12分) 。
解:(I) 曲线
曲线 在点( 0,
在点( 0, )处的切线与
)处的切线与 轴平行
轴平行 
 分
分

(II)由c=0,方程  可化为
可化为 
假没存在实数b使得此方程恰有一个实数根,

①
此方程恰有一个实根
②若b>o,则
 的变化情况如下
的变化情况如下


③若b<o,则
 的变化情况如下
的变化情况如下


综合①②③可得,实数b的取值范围是
(22)解:,
(Ⅰ)由题意设双曲线的标准方程为 
由已知得 

双曲线G的标准方程为 
(Ⅱ)


化简整理得,

www.ks5u.com
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com