查看答案和解析>>

查看答案和解析>>

已知函数，为的导函数。  （1）求函数的单调递减区间；
（2）若对一切的实数，有成立，求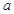的取值范围； 
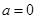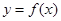（3）当时，在曲线上是否存在两点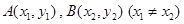，使得曲线在 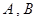两点处的切线均与直线交于同一点？若存在，求出交点纵坐标的最大值；若不存在，请说明理由．

查看答案和解析>>

查看答案和解析>>

已知函数 
(1)若在上是减函数，求的最大值；
(2)若的单调递减区间是，求函数y=图像过点的切线与两坐标轴围成图形的面积。

查看答案和解析>>

一、选择题：BADBD   CCCCA   BB 

二、填空题:13．    14．-80    15．-4或-26    16．―

三、解答题

17．（本小题满分10分）

 解：（1）         …………………………4分

又                  ……………………6分

(2)       

（当且仅当a=c时取到等号）

 ,的面积的最大值为    

18．（本小题满分12分）解：（1）甲取得的3个全是白球，则必胜，其概率为         

甲取得2个白球获胜是乙取得1个白球3个黑球或4个黑球的情况下发生的，其概率为

  甲取1 个白球获胜是在乙取得4 个黑球的情况下发生的，其概率为  由于这三个事件是互斥的，所以甲获胜的概率为    （2）对于平局的情况，只有甲取1白2黑而乙取1白3黑或甲取2白1黑而乙取2白2黑时才发生，前者的概率为                                               

后者的概率为       所以甲乙成平局的概率为      19．（本小题满分12分）

（1）证明：取中点，连接、．∵△是等边三角形，∴⊥，

       又平面⊥平面，∴⊥平面，∴在平面内射影是，∵=2，，，,

       ∴△∽△，∴．又°，∴°，∴°，∴⊥，由三垂线定理知⊥ 

（2）解：由⊥，⊥得是二面角的平面角  

       在Rt△中，，，∴，       °，∴二面角的大小是45°

（3）解：设到平面的距离距离是，则，

，，

．又，，

∴=，∴点到平面的距离距离是

20．（本小题满分12分）解：（1）因为；故 当时；；当时，；满足上式；所以；  

 又因为，所以数列为等差数列；

    由，，故；所以公差；

     所以：； …………5分

（2）  ……… 6分

∴  …8分 由于  ∴单调递增   ∴ 得  ∴   ………10分

21.（1）  由题意得

令由此可知

－1

3

+

0

－

0

+

ㄊ

极大值

ㄋ

极小值－9

ㄊ

时取极大值

（2）上是减函数

上恒成立

作出不等式组表示的平面区域如图

当直线经过点时 取最小值

有最小值

22．（本小题满分12分）

解：（1）设椭圆方程由题意知，

∴∴椭圆方程为…………………………4分

（2）证明：易求出椭圆的右焦点，…………………………………7分

设显然直线的斜率存在，设直线的方程为代入方程并整理，得…

∴

又

,

即

∴…所以，

    夺分有道：考试如何避免粗心失分

   ●很多高三学生都会抱怨自己太粗心，“这道题很简单，只是我看错了。”甚至有些考生会说，这次的数学模拟中有20多分是因为粗心失的分。其实这些问题并不仅仅是由于粗心，很可能是由于平时的学习不够认真，基本功不扎实。

    正确面对“粗心”失误:  高考中基础的内容占了大多数，也就是说大部分的题目都应该在能力范围之内，可是很少有人把自己会做的都做对了。往往高考得好的同学就是在考试中能严谨答题，少出失误的同学。考试不会给任何人解释的机会，错了就是错了。再说白了一点，粗心也是自己能力不够的表现。 所以考生在平时复习时就要重视这种问题。应该分析为什么会看错，是什么误导了自己，以后怎么才能避免。不要只关心答案正确与否，而不分析思考的过程和方法。因为答案并不是平时复习的目的，如何正确地导向答案才是平时练习中需要知道的。 严谨的态度还体现在书写是否规范上。有经验的老师和同学部知道，书写的规范与否，直接关系到考分的高低。特别是主观题，会做甚至是做对了答案，也不一定在这道题上得满分，原因就在于书写不规范，缺少必要的步骤。笔者建议同学们可以参考往年高考试题的标准答案，其中有很严谨的解题步骤和书写方式。这是我们需要掌握的。

    “粗心”失分的三大原因

    一是审题不清。有些同学在考试时发现某道题目与做多的某题类似，顿时兴奋，还没读完题目，或者还没充分掘出题目的隐含条件就急忙答题，而事实上，该题与以前的题目只是相似而己，有着本质的区别，答案自然是南辕北辙。只有读懂读正确了题目,才有可能得到正确的分析过程.怎么读好题目呢?我的经历告诉我,必须一个字一个字的读,千万不要遗漏,特别是数学符号，还有负号看漏了、单位弄混了、存在和任意混了、正整数条件看掉了等，所以，考试中千万不要在“审题”这个环节上省时间，审题审透了，解题自然快而顺手，仔细读完一道题目或许只多花了几分钟，但如果审错了题，损失的可不仅是时间，还有分数。

    审题要注意根据题目中的有关特征去联想，挖掘隐含条件，准确地找出题目的关键词与关键数据，从中获取尽可能多的信息，找有效的解题线索。

    二是运算不认真: 很多同学会说自己的难题都对了，简单的题目反倒错了。事实上，这跟答一题的态度有关。在遇到难题的时候，往往会对题目给予足够重视，全神贯注、专心致志地去解答，答题过程、步骤也比较详尽。计算过程,千万不要跳跃某一步骤(除非你有万无一失的把握),注意,这些内容一般是在草稿纸上完成的,最后在解答过程中的书写一般不要写计算过程.所以你一定要把这些过程写得明明白白,这为你回过头来检查提供的高效率高质量的保障.在解简单题目的时候，更不能掉以轻心，要稳、要准，尽量不要花时间回头检查做二遍题，步骤也尽量不要省略不要跳，结果错了一步也不容易发现，导致最后答题失误。

    这种现象也是平时学习不塌实的表现。平时不重视基础题的复习，好大喜功，专做难题、怪题，自认为这就是能力的提高。其实，高考主要考的还是基础知识，分值最多的也都在基础题上，考生一定要在最后阶段重点抓基础题的复习。

    三是临场紧张:有些考生在考场上总怕时间不够，前面的题目还没做好，就想着下一道题。前面的题太简单了过不做，太难了做不出来也跳过不做。结果，东一榔头西一棒，慌慌张张的，哪道题目都没有好好地做完，出错自然难免。

    这固然跟临场发挥有关，也跟平时做题习惯有关。很多同学在做题目的时候都有做一半的坏习惯，做了一个开头，认为自己会做了，就不做完整。长此以往，答题时就容易答不完全。

同学们在平时练习的是时候，要追求质，而不是量。不要忙着做很多题，而是要保证每道题目的总确性。