
题目列表(包括答案和解析)
(本小题满分12分)
已知函数![]()
(1)确定![]() 上的单调性;[来源:学科网]
上的单调性;[来源:学科网]
(2)设![]() 在(0,2)上有极值,求
在(0,2)上有极值,求![]() 的取值范围。
的取值范围。
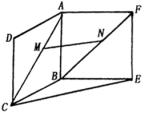
(本小题满分12分)如图,ABCD和ABEF都是正方形,![]() ,且
,且![]() .证明:
.证明:![]() 平面BCE.
平面BCE.
[来源:学&科&网]
(本小题满分12分)[来源:学科网ZXXK]
某校高三文科分为四个班.高三数学调研测试后,
随机地在各班抽取部分学生进行测试成绩统计,
各班被抽取的学生人数恰好成等差数列,人数最少的班被抽取了22人。
抽取出来的所有学生的测试成绩统计结果的频率分布条形图如图5所示,
其中120~130(包括120分但不包括130分)的频率为0.05,此 0
分数段的人数为5人![]()

(1)问各班被抽取的学生人数各为多少人?
(2)在抽取的所有学生中,任取一名学生, 求分数不小(![]() 本小题满分12分)
本小题满分12分)
(本小题满分12分)
如图所示,在正三棱柱![]() 中,底面边长为
中,底面边长为![]() ,侧棱长为
,侧棱长为![]() ,
,![]() 是棱
是棱![]() 的中点.
的中点.
| |
(Ⅱ)求二面角![]() 的大小;[来源:学科网ZXXK]
的大小;[来源:学科网ZXXK]
(Ⅲ)求点![]() 到平面
到平面![]() 的距离.
的距离.
(本小题满分12分)
班主任为了对本班学生的考试成绩进行分析,决定从全班25位女同学,15位男同学中随机抽取一个容量为8的样本进行分析.
(1)如果按性别比例分层抽样,可以得到多少个不同的样本(只要求写出算式即可,不必计算出结果);
(2)随机抽取8位同学,数学分![]() 数依次为:60,65,70,75,80,85,90,95;
数依次为:60,65,70,75,80,85,90,95;
物理成绩依次为:72,77,80,84,88,90,93,95,
①若规定90分(含90分)以上为优秀,记![]() 为这8位同学中数学和物理分数均为优秀的人数,求
为这8位同学中数学和物理分数均为优秀的人数,求![]() 的分布列和数学期望;
的分布列和数学期望;
②若这8位同学的数学、物理分数事实上对应下表:
| 学生编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7[来源:Z#xx#k.Com] | 8 |
| 数学分数 | 60 | 65 | 70 | 75 | 80 | 85 | 90 | 95 |
| 物理分数 | 72 | 77 | 80[来源:学科网] | 84 | 88 | 90 | 93 | 95 |
根据上表数据可知,变量![]() 与
与![]() 之间具有较强的线性相关关系,求出
之间具有较强的线性相关关系,求出![]() 与
与![]() 的线性回归方程(系数精确到0.01).(参考公式:
的线性回归方程(系数精确到0.01).(参考公式:![]() ,其中
,其中 ,
,![]() ;参考数据:
;参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)
一、选择题:CADBD DCABD AB.files/image007.jpg) 学科网
学科网
二、填空题:.files/image007.jpg) 学科网
学科网
13.甲; 14.6,6; 15..files/image080.gif) =0或
=0或.files/image114.gif) ; 16.一个点(1,1),(1,1)。
; 16.一个点(1,1),(1,1)。.files/image007.jpg) 学科网
学科网
三、解答题:.files/image007.jpg) 学科网
学科网
17.(1)①若切线的斜率存在,可设切线的方程为.files/image007.jpg) 学科网
学科网
.files/image116.gif) 即
即.files/image118.gif)
.files/image007.jpg) 学科网
学科网
则圆心到切线的距离 .files/image120.gif)
.files/image007.jpg) 学科网
学科网
解得 .files/image122.gif)
.files/image007.jpg) 学科网
学科网
故切线的方程为.files/image124.gif) ………………………………………………4分
………………………………………………4分.files/image007.jpg) 学科网
学科网
②若切线的斜率不存在,切线方程为.files/image028.gif) =2,此时直线也与圆相切
=2,此时直线也与圆相切
综上所述,过P点的切线的方程为.files/image124.gif) 和
和.files/image028.gif) =2…………………8分
=2…………………8分
(2)又设圆心C(1,1),则PC=.files/image129.gif) ;
;
所以切线长为.files/image131.gif) 。…………………………l2分
。…………………………l2分
18.解:设直线.files/image054.gif) 夹在直线
夹在直线.files/image009.gif) ,
,.files/image011.gif) 之间的线段是AB,且被点P(3,0)平分。设点A,B的坐标分别是(
之间的线段是AB,且被点P(3,0)平分。设点A,B的坐标分别是(.files/image136.gif) ),(
),(.files/image138.gif) ),所以
),所以
.files/image140.gif) ,
,.files/image142.gif)
于是.files/image144.gif) ,
,.files/image146.gif) …………………………………………………4分
…………………………………………………4分
由于点A,B分别在直线.files/image009.gif) ,
,.files/image011.gif) 上,所以
上,所以
.files/image148.gif)
解得.files/image150.gif) ,
,.files/image152.gif) ,即点A的坐标是(
,即点A的坐标是(.files/image154.gif) )……………………………8分
)……………………………8分
直线PA的方程为.files/image156.gif) 即
即.files/image158.gif)
所以,直线.files/image054.gif) 的方程是
的方程是.files/image158.gif) ………………………………………12分
………………………………………12分
19.解:(1)
.files/image162.jpg) …………………3分
…………………3分
(2)
序号
.files/image028.gif)
.files/image101.gif)
.files/image166.gif)
.files/image168.gif)
l
3
2.5
7.5
9
2
4
3
12
16
3
5
4
20
25
4
6
4.5
27
36
.files/image170.gif)
18
14
66.5
86
………………………6分
所以:
.files/image172.gif)
.files/image174.gif)
所以线性同归方程为:.files/image176.gif) ………………………………9分
………………………………9分
(3).files/image028.gif) =100时,
=100时,.files/image179.gif) ,所以预测生产100吨甲产品的生产能耗比技术改造前降低19.65吨标准煤…………………………………………………12分
,所以预测生产100吨甲产品的生产能耗比技术改造前降低19.65吨标准煤…………………………………………………12分
20.(1)当循环 ………………………………………………………2分
(2)①处应填.files/image050.gif) ≤30;②处应填
≤30;②处应填.files/image182.gif) ; …………………………8分
; …………………………8分
(3)程序
.files/image184.gif)
p=1
s=0
WHILE .files/image050.gif) <=30
<=30
s=s+p
p=p+i
i=i+1
WEND
PRINT s
END
(第20题程序)
………………………………12分
21.(1)
分组
频数
频率
频率/组距
[19.5,29.5]
4
0.2
0.02
[29.5,39.5]
4
0.2
0.02
[39.5,49.5]
6
0.3
0.03
[49.5,59.5]
6
0.3
0.03
合计
20
1
0.1
……………………………4分
(2)
.files/image187.jpg)
…………………………8分
(3)估计平均数:0.2×24.5+0.2×34.5+0.3×44.5+0.3×54.5=41.5
实际平均数:41.65
误差:0.15 …………………………………………………12分
22.解(1)设A(.files/image136.gif) ),M(
),M(.files/image190.gif) ),………………………………………………2分
),………………………………………………2分
由中点公式得.files/image192.gif)
.files/image194.gif) ………………………………4分
………………………………4分
因为A在圆C上,所以.files/image196.gif) ,即
,即.files/image198.gif) ……………6分
……………6分
点M的轨迹是以.files/image200.gif) 为圆心,1为半径的圆………………………………………8分
为圆心,1为半径的圆………………………………………8分
(2)设L的斜率为.files/image202.gif) ,则L的方程为
,则L的方程为.files/image204.gif) 即
即.files/image206.gif) ………10分
………10分
因为CA⊥CD,△CAD为等腰直角三角形,
圆心C(-1,0)到L的距离为.files/image208.gif) CD=
CD=.files/image210.gif)
由点到直线的距离公式得.files/image212.gif) ∴
∴.files/image214.gif) ………12分
………12分
∴.files/image216.gif) 解得
解得.files/image218.gif) ………………………………………4分
………………………………………4分
说明:其它答案相应给发,也可根据实际细化评分标准。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com