
题目列表(包括答案和解析)
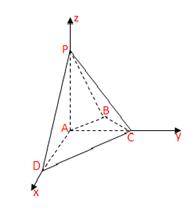
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AC⊥AD,AB⊥BC,∠BAC=45°,PA=AD=2,AC=1.
(Ⅰ)证明PC⊥AD;
(Ⅱ)求二面角A-PC-D的正弦值;
(Ⅲ)设E为棱PA上的点,满足异面直线BE与CD所成的角为30°,求AE的长.
【解析】解法一:如图,以点A为原点建立空间直角坐标系,依题意得A(0,0,0),D(2,0,0),C(0,1,0), 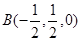 ,P(0,0,2).
,P(0,0,2).
(1)证明:易得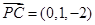 ,
,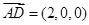 于是
于是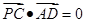 ,所以
,所以
(2) 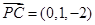 ,
,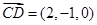 设平面PCD的法向量
设平面PCD的法向量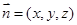 ,
,
则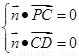 ,即
,即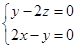 .不防设
.不防设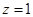 ,可得
,可得 .可取平面PAC的法向量
.可取平面PAC的法向量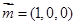 于是
于是 从而
从而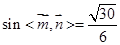 .
.
所以二面角A-PC-D的正弦值为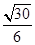 .
.
(3)设点E的坐标为(0,0,h),其中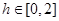 ,由此得
,由此得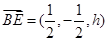 .
.
由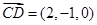 ,故
,故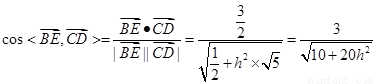
所以, ,解得
,解得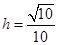 ,即
,即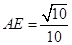 .
.
解法二:(1)证明:由 ,可得
,可得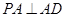 ,又由
,又由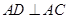 ,
,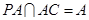 ,故
,故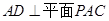 .又
.又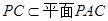 ,所以
,所以 .
.

(2)如图,作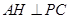 于点H,连接DH.由
于点H,连接DH.由 ,
,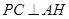 ,可得
,可得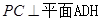 .
.
因此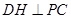 ,从而
,从而 为二面角A-PC-D的平面角.在
为二面角A-PC-D的平面角.在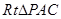 中,
中,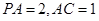 ,由此得
,由此得 由(1)知
由(1)知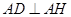 ,故在
,故在 中,
中,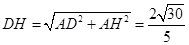
因此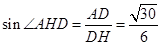 所以二面角
所以二面角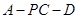 的正弦值为
的正弦值为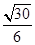 .
.
(3)如图,因为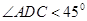 ,故过点B作CD的平行线必与线段AD相交,设交点为F,连接BE,EF. 故
,故过点B作CD的平行线必与线段AD相交,设交点为F,连接BE,EF. 故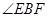 或其补角为异面直线BE与CD所成的角.由于BF∥CD,故
或其补角为异面直线BE与CD所成的角.由于BF∥CD,故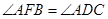 .在
.在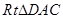 中,
中, 故
故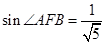
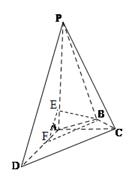
在 中,由
中,由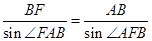 ,
,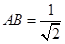 ,
,
可得 .由余弦定理,
.由余弦定理,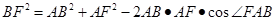 ,
,
所以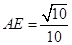 .
.
已知 ,函数
,函数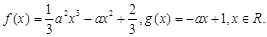
(1)当 时,求函数
时,求函数 在点(1,
在点(1,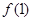 )的切线方程;
)的切线方程;
(2)求函数 在[-1,1]的极值;
在[-1,1]的极值;
(3)若在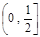 上至少存在一个实数x0,使
上至少存在一个实数x0,使 >g(xo)成立,求正实数
>g(xo)成立,求正实数 的取值范围。
的取值范围。
【解析】本试题中导数在研究函数中的运用。(1)中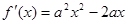 ,那么当
,那么当 时,
时,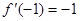 又
又  所以函数
所以函数 在点(1,
在点(1,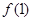 )的切线方程为
)的切线方程为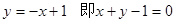 ;(2)中令
;(2)中令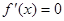 有
有 

对a分类讨论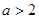 ,和
,和 得到极值。(3)中,设
得到极值。(3)中,设 ,
, ,依题意,只需
,依题意,只需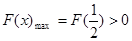 那么可以解得。
那么可以解得。
解:(Ⅰ)∵ ∴
∴ 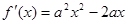
∴ 当 时,
时,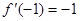 又
又 
∴ 函数 在点(1,
在点(1,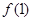 )的切线方程为
)的切线方程为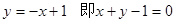 --------4分
--------4分
(Ⅱ)令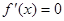 有
有 

①
当 即
即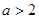 时
时
|
|
(-1,0) |
0 |
(0, |
|
( |
|
|
+ |
0 |
- |
0 |
+ |
|
|
|
极大值 |
|
极小值 |
|
故 的极大值是
的极大值是 ,极小值是
,极小值是
②
当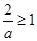 即
即 时,
时, 在(-1,0)上递增,在(0,1)上递减,则
在(-1,0)上递增,在(0,1)上递减,则 的极大值为
的极大值为 ,无极小值。
,无极小值。
综上所述  时,极大值为
时,极大值为 ,无极小值
,无极小值
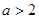 时 极大值是
时 极大值是 ,极小值是
,极小值是 ----------8分
----------8分
(Ⅲ)设 ,
,
对 求导,得
求导,得
∵ ,
,
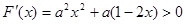
∴  在区间
在区间 上为增函数,则
上为增函数,则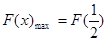
依题意,只需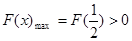 ,即
,即
解得 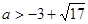 或
或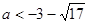 (舍去)
(舍去)
则正实数 的取值范围是(
的取值范围是(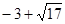
 ,
, )
)
设函数f(x)=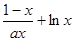 在[1,+∞
在[1,+∞ 上为增函数.
上为增函数.
(1)求正实数a的取值范围;
(2)比较 的大小,说明理由;
的大小,说明理由;
(3)求证: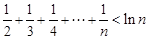 (n∈N*, n≥2)
(n∈N*, n≥2)
【解析】第一问中,利用
解:(1)由已知: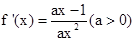 ,依题意得:
,依题意得: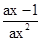 ≥0对x∈[1,+∞
≥0对x∈[1,+∞ 恒成立
恒成立
∴ax-1≥0对x∈[1,+∞ 恒成立 ∴a-1≥0即:a≥1
恒成立 ∴a-1≥0即:a≥1
(2)∵a=1 ∴由(1)知:f(x)= 在[1,+∞)上为增函数,
在[1,+∞)上为增函数,
∴n≥2时:f( )=
)=

(3) ∵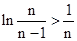 ∴
∴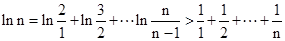
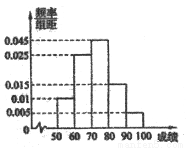
山东省《体育高考方案》于2012年2月份公布,方案要求以学校为单位进行体育测试,某校对高三1班同学按照高考测试项目按百分制进行了预备测试,并对50分以上的成绩进行统计,其频率分布直方图如图所示,若90~100分数段的人数为2人.
(Ⅰ)请估计一下这组数据的平均数M;
(Ⅱ)现根据初赛成绩从第一组和第五组(从低分段到高分段依次为第一组、第二组、…、第五组)中任意选出两人,形成一个小组.若选出的两人成绩差大于20,则称这两人为“帮扶组”,试求选出的两人为“帮扶组”的概率.
【解析】本试题主要考查了概率的运算和统计图的运用。
(1)由由频率分布直方图可知:50~60分的频率为0.1, 60~70分的频率为0.25, 70~80分的频率为0.45, 80~90分的频率为0.15, 90~100分的频率为0.05,然后利用平均值公式,可知这组数据的平均数M=55×0.1+65×0.25+75×0.45+85×0.15+95×0.05=73(分)
(2)中利用90~100分数段的人数为2人,频率为0.05;得到总参赛人数为40,然后得到0~60分数段的人数为40×0.1=4人,第五组中有2人,这样可以得到基本事件空间为15种,然后利用其中两人成绩差大于20的选法有:(A1,B1),(A1,B2),(A2,B1),(A2,B2),(A3,B1),(A3,B2),(A4,B1),(A4,B2)共8种,得到概率值
解:(Ⅰ)由频率分布直方图可知:50~60分的频率为0.1, 60~70分的频率为0.25, 70~80分的频率为0.45, 80~90分的频率为0.15, 90~100分的频率为0.05; ……………2分
∴这组数据的平均数M=55×0.1+65×0.25+75×0.45+85×0.15+95×0.05=73(分)…4分
(Ⅱ)∵90~100分数段的人数为2人,频率为0.05;
∴参加测试的总人数为 =40人,……………………………………5分
=40人,……………………………………5分
∴50~60分数段的人数为40×0.1=4人, …………………………6分
设第一组50~60分数段的同学为A1,A2,A3,A4;第五组90~100分数段的同学为B1,B2
则从中选出两人的选法有:(A1,A2),(A1,A3),(A1,A4),(A1,B1),(A1,B2),(A2,A3),(A2,A4),(A2,B1),(A2,B2),(A3,A4),(A3,B1),(A3,B2),(A4,B1),(A4,B2),(B1,B2),共15种;其中两人成绩差大于20的选法有:(A1,B1),(A1,B2),(A2,B1),(A2,B2),(A3,B1),(A3,B2),(A4,B1),(A4,B2)共8种 …………………………11分
则选出的两人为“帮扶组”的概率为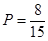
现有4个人去参加某娱乐活动,该活动有甲、乙两个游戏可供参加者选择.为增加趣味性,约定:每个人通过掷一枚质地均匀的骰子决定自己去参加哪个游戏,掷出点数为1或2的人去参加甲游戏,掷出点数大于2的人去参加乙游戏.
(Ⅰ)求这4个人中恰有2人去参加甲游戏的概率;
(Ⅱ)求这4个人中去参加甲游戏的人数大于去参加乙游戏的人数的概率;
(Ⅲ)用X,Y分别表示这4个人中去参加甲、乙游戏的人数,记 ,求随机变量
,求随机变量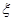 的分布列与数学期望
的分布列与数学期望 .
.
【解析】依题意,这4个人中,每个人去参加甲游戏的概率为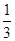 ,去参加乙游戏的概率为
,去参加乙游戏的概率为 .
.
设“这4个人中恰有i人去参加甲游戏”为事件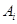
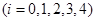
则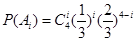 .
.
(1)这4个人中恰有2人去参加甲游戏的概率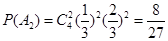
(2)设“这4个人中去参加甲游戏的人数大于去参加乙游戏的人数”为事件B,则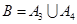 .由于
.由于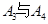 互斥,故
互斥,故
所以,这个人中去参加甲游戏的人数大于去参加乙游戏的人数的概率为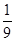 .
.
(3)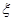 的所有可能取值为0,2,4.由于
的所有可能取值为0,2,4.由于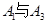 互斥,
互斥, 互斥,故
互斥,故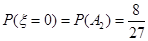
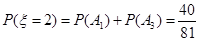

所以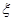 的分布列是
的分布列是
|
|
0 |
2 |
4 |
|
P |
|
|
|
随机变量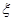 的数学期望
的数学期望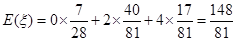 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com