
题目列表(包括答案和解析)
(12分)定义![]() 的“倒平均数”为
的“倒平均数”为![]() ,已知数列
,已知数列![]() 前
前![]() 项的“倒平均数”为
项的“倒平均数”为![]() .
.
(1)记![]() ,试比较
,试比较![]() 与
与![]() 的大小;
的大小;
(2)是否存在实数![]() ,使得当
,使得当![]() 时,
时,![]() 对任意
对任意![]() 恒成立?若存在,求出最大的实数
恒成立?若存在,求出最大的实数![]() ;若不存在,说明理由.
;若不存在,说明理由.
| n |
| x1+x2+…+xn |
| 1 |
| 2n+ 4 |
| an |
| n+1 |
| lim |
| n→∞ |
| n |
| x1+x2+…+xn |
| 1 |
| 2n+ 4 |
| an |
| n+1 |
| lim |
| n→∞ |
 (n∈N*).已知数列{an}前n项的“倒平均数”为
(n∈N*).已知数列{an}前n项的“倒平均数”为 ,记cn=
,记cn= (n∈N*).
(n∈N*). Tn.
Tn.(本题满分16分)定义 ,
, ,…,
,…, 的“倒平均数”为
的“倒平均数”为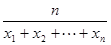 (
( ).已知数列
).已知数列 前
前 项的“倒平均数”为
项的“倒平均数”为 ,记
,记 (
( ).
).
(1)比较 与
与 的大小;
的大小;
(2)设函数 ,对(1)中的数列
,对(1)中的数列 ,是否存在实数
,是否存在实数 ,使得当
,使得当 时,
时, 对任意
对任意 恒成立?若存在,求出最大的实数
恒成立?若存在,求出最大的实数 ;若不存在,说明理由.
;若不存在,说明理由.
(3)设数列 满足
满足 ,
, (
( 且
且 ),
), (
( 且
且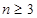 ),且
),且 是周期为
是周期为 的周期数列,设
的周期数列,设 为
为 前
前 项的“倒平均数”,求
项的“倒平均数”,求 .
.
1.B 2.D 3.A 4.B 5.C 6.D 7.A 8.B 9.C 10.C
11.2 12. /file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(6).files\image242.gif) 13.0 14.
13.0 14./file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(6).files\image244.gif) 15.96
15.96
16.解:(1)依题意:/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(6).files\image246.gif) ,即
,即/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(6).files\image248.gif) ,又
,又/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(6).files\image250.gif) ,
,
∴ /file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(6).files\image252.gif) ,∴
,∴ /file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(6).files\image254.gif) ,
,
(2)由三角形是锐角三角形可得/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(6).files\image256.gif) ,即
,即/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(6).files\image258.gif) 。
。
由正弦定理得/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(6).files\image260.gif) ∴
∴ /file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(6).files\image262.gif) ,
,/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(6).files\image264.gif)
∴ /file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(6).files\image266.gif) ,
,
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(6).files\image268.gif)
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(6).files\image270.gif)
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(6).files\image272.gif)
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(6).files\image274.gif)
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(6).files\image276.gif)
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(6).files\image278.gif)
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(6).files\image280.gif) ∵
∵ /file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(6).files\image281.gif) ,∴
,∴ /file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(6).files\image283.gif) ,
,
∴ /file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(6).files\image285.gif) 即
即/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(6).files\image287.gif) 。
。
17.设/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(6).files\image289.gif) ,则
,则/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(6).files\image291.gif) =
=/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(6).files\image293.gif) ,
,/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(6).files\image295.gif) ,
,
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(6).files\image297.gif) ,又
,又/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(6).files\image299.gif) ,
,
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(6).files\image301.gif) .
.
(2)/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(6).files\image303.gif) =
=/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(6).files\image305.gif) ,
,/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(6).files\image307.gif)
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(6).files\image309.gif)
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(6).files\image311.gif)
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(6).files\image313.gif)
18解:(1)记数列/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(6).files\image179.gif) 的前
的前/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(6).files\image181.gif) 项和为
项和为/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(6).files\image317.gif) ,则依题有
,则依题有/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(6).files\image319.gif)
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(6).files\image321.gif) ,故
,故/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(6).files\image323.gif)
故数列的通项为/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(6).files\image325.gif) .故
.故/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(6).files\image327.gif) ,易知,
,易知,/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(6).files\image329.gif) .
.
(2)假设存在实数/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(6).files\image191.gif) ,使得当
,使得当/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(6).files\image193.gif) 时,
时,/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(6).files\image195.gif) 对任意
对任意/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(6).files\image332.gif) 恒成立,则
恒成立,则/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(6).files\image334.gif) 对任意
对任意/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(6).files\image332.gif) 都成立,,
都成立,,/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(6).files\image336.gif)
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(6).files\image338.gif) ,
,
得/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(6).files\image340.gif) ,有
,有/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(6).files\image342.gif) 或
或/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(6).files\image344.gif) .故存在最大的实数
.故存在最大的实数/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(6).files\image346.gif) 符合题意.
符合题意.
19. 20. 解:设该学生选修甲、乙、丙的概率分别为x、y、z
依题意得/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(6).files\image348.gif)
(1)若函数/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(6).files\image350.gif) 为R上的偶函数,则
为R上的偶函数,则/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(6).files\image199.gif) =0
=0
当/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(6).files\image199.gif) =0时,表示该学生选修三门功课或三门功课都没选.
=0时,表示该学生选修三门功课或三门功课都没选.
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(6).files\image354.gif)
=0.4×0.5×0.6+(1-0.4)(1-0.5)(1-0.6)=0.24
∴事件A的概率为0.24
(2)依题意知/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(6).files\image199.gif) 的的取值为0和2由(1)所求可知
的的取值为0和2由(1)所求可知
P(/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(6).files\image199.gif) =0)=0.24 P(
=0)=0.24 P(/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(6).files\image199.gif) =2)=1- P(
=2)=1- P(/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(6).files\image199.gif) =0)=0.76
=0)=0.76
则/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(6).files\image199.gif) 的分布列为
的分布列为
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(6).files\image199.gif)
0
2
P
0.24
0.76
∴/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(6).files\image199.gif) 的数学期望为E
的数学期望为E/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(6).files\image199.gif) =0×0.24+2×0.76=1.52
=0×0.24+2×0.76=1.52
20. (1)由题意可知/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(6).files\image357.gif) ,又
,又/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(6).files\image359.gif) ,解得
,解得/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(6).files\image361.gif) ,
,
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(6).files\image363.gif) 椭圆的方程为
椭圆的方程为/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(6).files\image365.gif) ;
;
(2)由(1)得/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(6).files\image367.gif) ,所以
,所以/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(6).files\image369.gif) .假设存在满足题意的直线
.假设存在满足题意的直线/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(6).files\image140.gif) ,设
,设/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(6).files\image140.gif) 的方程为
的方程为
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(6).files\image373.gif) ,代入
,代入/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(6).files\image374.gif) ,得
,得/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(6).files\image376.gif) ,
,
设/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(6).files\image378.gif) ,则
,则/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(6).files\image380.gif) ①
①/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(6).files\image382.gif) ,
,
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(6).files\image384.gif) ,
,
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(6).files\image386.gif) 而
而/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(6).files\image388.gif) 的方向向量为
的方向向量为/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(6).files\image390.gif) ,
,
; /file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(6).files\image392.gif)
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(6).files\image363.gif) 当
当/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(6).files\image395.gif) 时,
时,/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(6).files\image397.gif) ,即存在这样的直线
,即存在这样的直线/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(6).files\image140.gif) ;
;
当/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(6).files\image400.gif) 时,
时,/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(6).files\image063.gif) 不存在,即不存在这样的直线
不存在,即不存在这样的直线/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(6).files\image140.gif) .
.
21.(1) 必要性 :/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(6).files\image404.gif) ,又
,又 /file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(6).files\image406.gif) ,即
,即/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(6).files\image234.gif)
充分性 :设 /file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(6).files\image234.gif) ,对
,对/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(6).files\image232.gif) 用数学归纳法证明
用数学归纳法证明/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(6).files\image230.gif)
当/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(6).files\image411.gif) 时,
时,/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(6).files\image413.gif) .假设
.假设/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(6).files\image415.gif)
则/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(6).files\image417.gif) ,且
,且/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(6).files\image419.gif)
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(6).files\image421.gif) ,由数学归纳法知
,由数学归纳法知/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(6).files\image230.gif) 对所有
对所有/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(6).files\image232.gif) 成立
成立
(2) 设
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(6).files\image236.gif) ,当
,当/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(6).files\image411.gif) 时,
时,/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(6).files\image425.gif) ,结论成立
,结论成立
当/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(6).files\image427.gif) 时,
时, /file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(6).files\image429.gif)
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(6).files\image431.gif) ,由(1)知
,由(1)知/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(6).files\image433.gif) ,所以
,所以 /file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(6).files\image435.gif) 且
且 /file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(6).files\image437.gif)
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(6).files\image439.gif)
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(6).files\image441.gif)
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(6).files\image443.gif)
(3) 设 /file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(6).files\image236.gif) ,当
,当/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(6).files\image411.gif) 时,
时,/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(6).files\image445.gif) ,结论成立
,结论成立
当/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(6).files\image427.gif) 时,由(2)知
时,由(2)知/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(6).files\image448.gif)
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(6).files\image450.gif)
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(6).files\image452.gif)
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr1\d9fed872da573c75bec6fc4534da56c7.zip\65663\新建文件夹%20(3)\湖北省黄冈市09届高三数学理科二轮复习交流试题(6).files\image454.gif) w.w.w.k.s.5.u.c.o.m
w.w.w.k.s.5.u.c.o.m
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com