
题目列表(包括答案和解析)
 ,点P(2,-1)在矩阵A对应的变换下得到点P′(5,1),求矩阵A.
,点P(2,-1)在矩阵A对应的变换下得到点P′(5,1),求矩阵A.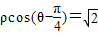 ,曲线C的参数方程为
,曲线C的参数方程为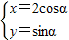 (α为参数),求曲线C截直线l所得的弦长.
(α为参数),求曲线C截直线l所得的弦长.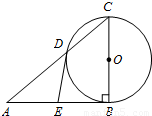
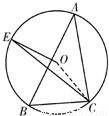
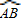 于点E,连接EC,求∠OEC.
于点E,连接EC,求∠OEC.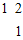 ]的作用下变换为曲线C2,求C2的方程.
]的作用下变换为曲线C2,求C2的方程.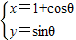 (θ为参数)上一点,求它到直线C2:
(θ为参数)上一点,求它到直线C2: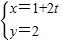 (t为参数)距离的最小值.
(t为参数)距离的最小值.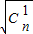 +
+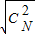 +L+
+L+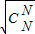 ≤
≤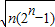 .
.
a、b、c为非零向量,l、m为实数,则命题:①b=la可推出a、b共线;②a、b共线可推出a=lb;③a、b、c在同一平面内,可推出a=lb+mc。其中真命题个数为( )
A.0 B.1 C.2 D.3
A.0 B.1 C.2 D.3
a、b是两条异面直线,它们所成的角为80°,过空间任一点P,作直线l,使l与a,b所成角均为50°,这样的l共有几条
A.1条
B.2条
C.3条
D.4条
一、选择题:本题考查基础知识和基本运算. 每题5分,满分60分.
1.D 2。C 3.C 4.A 5.B 6.D
7.A 8.B 9.A 10.C 11.B 12.A
二、填空题:本题考查基础知识和基本运算. 每题4分,满分16分.
13.15 14.4 15 . 16
16 
三、解答题:本题共6大题,共74分.解答应写出文字说明、证明过程或演算步骤.
17.本题主要考查三角函数性质、三角恒等变换等基本知识,考查推理和运算能力.
解:( I )

(Ⅱ)

18.本题主要考查简单随机抽样,用古典概型计算事件发生的概率等基础知识,考查研究基本事件的能力,以及应用意识。
解:(I)设红色球有 个,依题意得
个,依题意得 红色球有4个.
红色球有4个.
(II)记“甲取出的球的编号比乙的大”为事件A
所有的基本事件有(红1,白1),(红l,蓝2),(红1,蓝3),(白l,红1),
(白1,蓝2),(白1,蓝3),(蓝2,红1),(蓝2,自1),(蓝2,蓝3),
(蓝3,红1),(蓝3,白1),(蓝3,蓝2),共12个
事件A包含的基本事件有(蓝2,红1),(蓝2,白1),
(蓝3,蓝2),共5个
所以,

19.本题主要考查线面平行与垂直关系,及多面体的体积计算等基础知识,考查空间想象能力,逻辑思维能力和运算能力.
(I)解:取CD的中点为F,连EF,则EF为 的中位线.
的中位线.
 EF∥A
EF∥A
又EF  平面A1BC,.
平面A1BC,. EF∥平面A1BC
EF∥平面A1BC
 (II)证:四边形ABCD为直角梯形且AD∥BC,
(II)证:四边形ABCD为直角梯形且AD∥BC,
AB⊥BC,AD=2,AB=_BC=1. AC=CD=
AC=CD=  ,
,
 AD2=AC2+CD2 即
AD2=AC2+CD2 即 为直角三角形 CD⊥AC又四棱 柱ABCD一A1B
为直角三角形 CD⊥AC又四棱 柱ABCD一A1B
CD  底面ABCD
底面ABCD  AAl⊥CD,又AA1与AC交于点A,
AAl⊥CD,又AA1与AC交于点A,
 CD⊥平面A1ACCl
CD⊥平面A1ACCl
由CD⊥平面AlACCl, CD为四棱锥D-A1ACCl的底面 A1ACCl上的高,
CD为四棱锥D-A1ACCl的底面 A1ACCl上的高,
又AAl垂直于底面ABCD, 四边形A1ACC1为矩形
四边形A1ACC1为矩形
 四棱锥D―A1ACCI的体积
四棱锥D―A1ACCI的体积
20.此题主要考查数列、等差、等比数列的概念、数列的递推公式、数列前n项和的求法
同时考查学生的分析问题与解决问题的能力,逻辑推理能力及运算能力.
解:(I)

(Ⅱ)
 21.本题主要考查直线方程与性质、椭圆方程与性质以及直线与曲线的位置关系等基础知
21.本题主要考查直线方程与性质、椭圆方程与性质以及直线与曲线的位置关系等基础知
识;考查考生数形结合思想、运算求解能力、推理论证能力。
解:(I)

(Ⅱ)

22.本题主要考查二次函数及其性质、导数的基本知识,几何意义及其应用,同时考查考生分类讨论思想方法及化规的能力:
解:(Ⅰ)

(Ⅱ)

(Ⅲ)

① 

② 
③ 

方程 有两个不等的正根,存在两条满足条件的切线;
有两个不等的正根,存在两条满足条件的切线;


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com