
题目列表(包括答案和解析)
已知![]()
(Ⅰ)若![]() 求
求![]() 的表达式;
的表达式;
(Ⅱ)若函数f (x)和函数g(x)的图象关于原点对称,求函数g(x)的解析式;
(Ⅲ)若![]() 在
在![]() 上是增函数,求实数l的取值范围
上是增函数,求实数l的取值范围
已知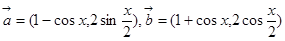 ,
,
设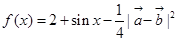 .
.
(Ⅰ)求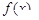 的表达式;
的表达式;
(Ⅱ)若函数 和函数
和函数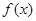 的图象关于原点对称,
的图象关于原点对称,
(ⅰ)求函数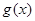 的解析式;
的解析式;
(ⅱ)若函数 在区间
在区间 上是增函数,求实数l的取值范围.
上是增函数,求实数l的取值范围.
已知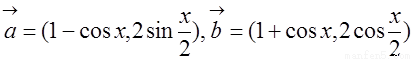
(Ⅰ)若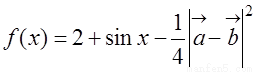 ,求
,求 的表达式;
的表达式;
(Ⅱ)若函数 和函数
和函数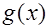 的图象关于原点对称,求函数
的图象关于原点对称,求函数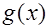 的解析式;
的解析式;
(Ⅲ)若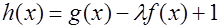 在
在 上是增函数,求实数
上是增函数,求实数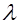 的取值范围.
的取值范围.
已知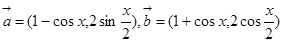
(Ⅰ)若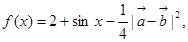 求
求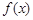 的表达式;
的表达式;
(Ⅱ)若函数f (x)和函数g(x)的图象关于原点对称,求函数g(x)的解析式;
(Ⅲ)若 在
在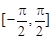 上是增函数,求实数l的取值范围.
上是增函数,求实数l的取值范围.
已知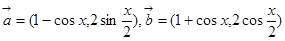 ,
,
设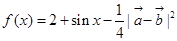 .
.
(Ⅰ)求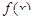 的表达式;
的表达式;
(Ⅱ)若函数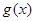 和函数
和函数 的图象关于原点对称,
的图象关于原点对称,
(ⅰ)求函数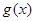 的解析式;
的解析式;
(ⅱ)若函数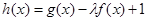 在区间
在区间 上是增函数,求实数l的取值范围.
上是增函数,求实数l的取值范围.
1. .files/image209.gif) 2.
2. .files/image211.gif) 3.
3..files/image213.gif) 4.
4..files/image215.gif) 5.
5..files/image217.gif) 6.(文)
6.(文).files/image219.gif) (理)
(理).files/image221.gif)
7..files/image223.gif) 8. 4 9.(文)
8. 4 9.(文).files/image225.gif) (理)1 10.
(理)1 10..files/image227.gif) 11.
11..files/image229.gif)
12-15. C A A B
16. (1).files/image231.gif) .
.
(2)取.files/image233.gif) 的中点
的中点.files/image235.gif) ,所求的角的大小等于
,所求的角的大小等于.files/image237.gif) 的大小,
的大小,
.files/image239.gif) 中
中.files/image241.gif) ,所以
,所以.files/image122.gif) 与底面
与底面.files/image124.gif) 所成的角的大小是
所成的角的大小是.files/image243.gif) .
.
17. (1)由函数.files/image245.gif) 的图像与x轴的任意两个相邻交点间的距离为
的图像与x轴的任意两个相邻交点间的距离为.files/image247.gif) 得函数周期为
得函数周期为.files/image249.gif) ,
,
.files/image251.gif)
.files/image253.gif) 直线
直线.files/image255.gif) 是函数
是函数.files/image245.gif) 图像的一条对称轴,
图像的一条对称轴,.files/image257.gif) ,
,
.files/image259.gif) 或
或.files/image261.gif) ,
,.files/image263.gif) ,
, .files/image265.gif) ,
, .files/image267.gif) .
. .files/image269.gif) .
.
(2).files/image271.gif)
.files/image273.gif)
.files/image275.gif) ,
,
即函数.files/image277.gif) 的单调递增区间为
的单调递增区间为.files/image279.gif) .
.
18. (1)第.files/image195.gif) 天销售的件数为
天销售的件数为.files/image282.gif)
则.files/image284.gif)
则:.files/image286.gif)
解得.files/image288.gif) ,即
,即
(2).files/image288.gif) 时,
时,.files/image290.gif) ,即未流行
,即未流行
.files/image292.gif) 时,
时,.files/image294.gif)
即从
当.files/image296.gif) 时,
时,.files/image298.gif) ,令
,令.files/image300.gif) ,解得
,解得.files/image302.gif)
即从
19. (1).files/image304.gif)
(2) 妨设.files/image147.gif) 在第一象限,则
在第一象限,则.files/image307.gif)
.files/image309.gif)
(3)若直线斜率存在,设为.files/image311.gif) ,代入
,代入.files/image304.gif)
得.files/image313.gif)
若平行四边形.files/image164.gif) 为矩形,则
为矩形,则.files/image316.gif)
.files/image318.gif)
.files/image320.gif)
.files/image322.gif) 无解
无解
若直线垂直.files/image324.gif) 轴,则
轴,则.files/image326.gif) 不满足.
不满足.
故不存在直线.files/image155.gif) ,使
,使.files/image164.gif) 为矩形.
为矩形.
20. 解:(1)由题意的:f ?1(x)=.files/image330.gif) = f(x)=
= f(x)=.files/image332.gif) ,所以p = ?1,所以an=
,所以p = ?1,所以an=.files/image334.gif) 翰林汇
翰林汇
(2) an=.files/image334.gif) ,dn=
,dn=.files/image336.gif) =n,
=n,
Sn为数列{dn}的前n项和,Sn=.files/image338.gif) ,又Hn为数列{Sn}的调和平均数,
,又Hn为数列{Sn}的调和平均数,
Hn=.files/image340.gif) =
=.files/image342.gif) =
=.files/image344.gif)
.files/image201.gif) =
=.files/image347.gif) =
=.files/image219.gif)
(3)因为正数数列{cn}的前n项之和Tn=.files/image219.gif) (cn+
(cn+.files/image351.gif) ),
),
所以c1=.files/image219.gif) (c1+
(c1+.files/image353.gif) ),解之得:c1=1,T1=1
),解之得:c1=1,T1=1
当n≥2时,cn = Tn?Tn?1,所以2Tn = Tn?Tn?1 +.files/image355.gif) ,
,
Tn +Tn?1 = .files/image355.gif) ,即:
,即:.files/image358.gif) = n,
= n,
所以,.files/image360.gif) = n?1,
= n?1,.files/image362.gif) = n?2,……,
= n?2,……,.files/image364.gif) =2,累加得:
=2,累加得:
.files/image366.gif) =2+3+4+……+ n,
=2+3+4+……+ n, .files/image368.gif) =1+2+3+4+……+ n =
=1+2+3+4+……+ n =.files/image370.gif) ,Tn=
,Tn=.files/image372.gif)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com