练习册

  • 练习册
  • 试题
    (2)设曲线C与y轴的正半轴的交点为M.过点M作一条直线l与曲线C交于另一点N.当|MN|=时.求直线l的方程. 【查看更多】

     

    题目列表(包括答案和解析)

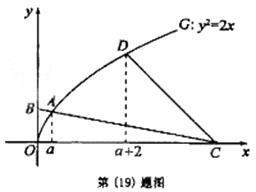
    如图，曲线G的方程为y2=2x（y≥0）.以原点为圆心，以t（t >0）为半径的圆分别与曲线G和y轴的正半轴相交于点A与点B.直线AB与x轴相交于点C.

    （Ⅰ）求点A的横坐标a与点C的横坐标c的关系式；

    （Ⅱ）设曲线G上点D的横坐标为a＋2，求证：直线CD的斜率为定值.

    查看答案和解析>>

    19.如图，曲线G的方程为y2=2x（y≥0）.以原点为圆心，以t（t ＞0）为半径的圆分别与曲线G和y轴的正半轴相交于点A与点B.直线AB与x轴相交于点C.

    （Ⅰ）求点A的横坐标a与点C的横坐标c的关系式；

    （Ⅱ）设曲线G上点D的横坐标为a＋2，求证：直线CD的斜率为定值.

    查看答案和解析>>

    如图，曲线G的方程为y2=20（y≥0）.以原点为圆心，以t（t >0）为半径的圆分别与曲线G和y轴的正半轴相交于点A与点B.直线AB与x轴相交于点C.

    （Ⅰ）求点A的横坐标a与点C的横坐标c的关系式；

    （Ⅱ）设曲线G上点D的横坐标为a＋2，求证：直线CD的斜率为定值.

    查看答案和解析>>

    如图，曲线G的方程为y2=2x（y≥0）.以原点为圆心，以t（t >0）为半径的圆分别与曲线G和y轴的正半轴相交于点A与点B，直线AB与x轴相交于点C。
    （1）求点A的横坐标a与点C的横坐标c的关系式；
    （2）设曲线G上点D的横坐标为a+2，求证：直线CD的斜率为定值。

    查看答案和解析>>

    （1）以直角坐标系的原点为极点，x轴的正半轴为极轴，并在两种坐标系中取相同的长度单位．已知直线的极坐标方程为θ=
    π
    4
    (ρ∈R)    ，它与曲线
    x=2+
    		5
    cosθ
    y=1+
    		5
    sinθ
    (θ    为参数）相交于两点A和B，求|AB|．
    （2）在直角坐标系xOy中，直线L的参数方程为
    x=3-
    		5
    5
    t
    y=-2+
    2
    		5
    5
    t
    （t为参数），在极坐标系（与直角坐标系xOy取相同的长度单位，且以原点O为极点，以x轴正半轴为极轴）中，圆C的方程为ρ=4cosθ．设圆C与直线L交于点A、B．若点P的坐标为（3，-2），求|PA|+|PB|及|PA|•|PB|．

    查看答案和解析>>

    一． 单项选择题

    题号

    1

    2

    3

    4

    5

    6

    7

    8

    9

    10

    答案

    D

    A

    C

    D

    B

    D

    A

    B

    D

    C

    二．填空题

    11、 5           12、25           13、         14、

    15、29π    

    三、解答题：

    16、解：(1)

                    =…………….4分

    的最小正周期为           ……………5分

    的对称中心为      …………….6分

    (2)   

     ……………..8分

    又 

    而      由     ……………10分   

                         ……………….12分

    17、解：(1)五项指标检测相当于5次独立重复试验，当有二项及二项以上不合格时，该批食品不能出厂，故不能出厂的概率为：

            ……………………………….4分

    或

    (2)若须五项全部检测完毕，才能确定能否出厂，则相当于前四项检测中恰有一项不合格的情形，故所求概率为：

       …………………………………..8分

            (3)由(1)知该批食品能出厂的概率为0.74不能出厂的概率为0.26

              故该厂生产一批食品获利的分布列为

    10000

    －5000

    0.74

    0.26

                                                          ….………….10分

    获利的期望为 …………..12分

    18、解：（1）由已知

       …………2分

    ∵    ∴             ……4分

    即所求曲线方程是：                           …………6分

    （2）由（1）求得点M（0，1）。显然直线l与x轴不垂直。

    故可设直线l的方程为y=kx+1 ，设M， N      …………8分

    由   消去y得：  解得  

    由

    解得：k=±1  ………………11分                             …………12分

    ∴所求直线的方程为                …………14分

    19, 解：解法一：（1）∵BF⊥平面ACE。  ∴BF⊥AF

    ∵二面角D―AB―E为直二面角。且CB⊥AB。

    ∴CB⊥平面ABE   ∴CB⊥AE   ∴AE⊥平面BCE           ……………4分

    （2）连结BD交AC交于G，连结FG

    ∵正方形ABCD边长为2。∴BG⊥AC  BG=

    ∵BF⊥平面ACE。  由三垂线定理的逆定理得

    FG⊥AC。  ∴∠BGF是二面B―AC―E的平面角              …………7分

    由（1）和AE⊥平面BCE

    又∵AE=EB

    ∴在等腰直角三角形AEB中，BE=

    又∵Rt△BCE中，

      ∴Rt△BFG中

    ∴二面角B―AC―E的正弦值等于                        ……………10分

    （3）过点E作ED⊥AB交AB于点O，  OE=1

    ∵二面角D―AB―E为直二面角    ∴EO⊥平面ABCD

    设点D到平面ACE的距离为h。   ∵VD-ACE=VE-ACD

    ∴

    即点D到平面ACE的距离为                          ………………14分

     

    20、解：(1)由 即  有唯一解

    又  

                                     …………4分

    (2)由                 …………6分

    又  

    数列 是以首项为，公差为的等差数列          …………8 分

                     ………10分

    (3)由       …………12分

    =

                  

                  

                                                  …………14分

    21、解：2．解：（Ⅰ）由条件得矩阵，

    它的特征值为和，对应的特征向量为及；

    （Ⅱ），椭圆在的作用下的新曲线的方程为．（7分）

    3．（坐标系与参数方程）求直线（）被曲线所截的弦长，将方程，分别化为普通方程：

    ，………(4分)

    ……(7分)

     

     

     

     

     


    同步练习册答案