
题目列表(包括答案和解析)
已知![]() 是定义在R上的偶函数,且对2为周期,则“
是定义在R上的偶函数,且对2为周期,则“![]() 上的增函数”是“
上的增函数”是“![]() 上的减函数”的
上的减函数”的
A.既不充分也不必要的条件 B.充分而不必要的条件
C.必要而不充分的条件 D.充要条件
已知 是定义在R上的偶函数,且对任意
是定义在R上的偶函数,且对任意 ,都有
,都有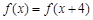 ,当
,当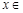
 时,
时,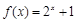 ,则函数
,则函数 在区间
在区间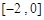 上的反函数
上的反函数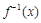 的值
的值
(A) (B)
(B) (C)
(C)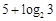 (D)
(D)
已知 是定义在R上的偶函数,且对任意
是定义在R上的偶函数,且对任意 ,都有
,都有 ,当
,当 [4,6]时,
[4,6]时, ,则函数
,则函数 在区间[-2,0]上的反函数
在区间[-2,0]上的反函数 的值
的值 为( )
为( )
A. B.
B.
C. D.
D.
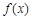 是定义在R上的偶函数,且对任意
是定义在R上的偶函数,且对任意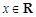 ,都有
,都有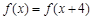 ,当
,当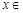
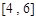 时,
时,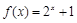 ,则函数
,则函数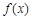 在区间
在区间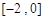 上的反函数
上的反函数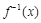 的值
的值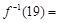
A.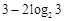 | B.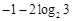 | C.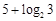 | D.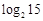 |
已知![]() 是定义在R上的偶函数,且对任意
是定义在R上的偶函数,且对任意![]()
![]() ,都有
,都有![]() ,当
,当![]()
![]() [4,6]时,
[4,6]时,![]() =2
=2![]() +1,则函数
+1,则函数![]() 在区间[一2,0]上的反函数
在区间[一2,0]上的反函数![]() 的值为
的值为
A.log215 B.3―2log23 C.5+log23 D.一1―2log23
1.A 2.B 3.B 4.D 5.(理)C (文)A 6.B 7.A 8.B 9.A
10.B 11.(理)A (文)C 12.B 13.(理) (文)25,60,15
(文)25,60,15
14.-672 15.2.5小时 16.①,④
17.解析:设f(x)的二次项系数为m,其图象上两点为(1-x, )、B(1+x,
)、B(1+x, )因为
)因为 ,
, ,所以
,所以 ,由x的任意性得f(x)的图象关于直线x=1对称,若m>0,则x≥1时,f(x)是增函数,若m<0,则x≥1时,f(x)是减函数.
,由x的任意性得f(x)的图象关于直线x=1对称,若m>0,则x≥1时,f(x)是增函数,若m<0,则x≥1时,f(x)是减函数.
∵  ,
, ,
, ,
, ,
, ,
,
 ,
,
∴ 当 时,
时,




 ,
, .
.
∵  , ∴
, ∴  .
.
当 时,同理可得
时,同理可得 或
或 .
.
综上: 的解集是当
的解集是当 时,为
时,为 ;
;
当 时,为
时,为 ,或
,或 .
.
18.解析:(理)(1)设甲队在第五场比赛后获得冠军为事件M,则第五场比赛甲队获胜,前四场比赛甲队获胜三场
依题意得 .
.
(2)设甲队获得冠军为事件E,则E包含第四、第五、第六、第七场获得冠军四种情况,且它们被彼此互斥.
∴  .
.
(文)设甲袋内恰好有4个白球为事件B,则B包含三种情况.
①甲袋中取2个白球,且乙袋中取2个白球,②甲袋中取1个白球,1个黑球,且乙袋中取1个白球,1个黑球,③甲、乙两袋中各取2个黑球.
∴ 
 .
.
19.解析:(甲)(1)建立如图坐标系:O为△ABC的重心,直线OP为z轴,AD为y轴,x轴平行于CB,
得A(0, ,0)、B(1,
,0)、B(1, ,0)、D(0,
,0)、D(0, ,0)、E(0,
,0)、E(0, ,
, ).
).
(2) ,
, ,
, ,
, ,
, ,
,
设AD与BE所成的角为 ,则
,则 .
.
∴  .
.

(乙)(1)取 中点E,连结ME、
中点E,连结ME、 ,
,
∴ 

 ,MC
,MC EC. ∴
EC. ∴ 
 MC. ∴
MC. ∴  ,M,C,N四点共面.
,M,C,N四点共面.

(2)连结BD,则BD是 在平面ABCD内的射影.
在平面ABCD内的射影.
∵  , ∴ Rt△CDM~Rt△BCD,∠DCM=∠CBD.
, ∴ Rt△CDM~Rt△BCD,∠DCM=∠CBD.
∴ ∠CBD+∠BCM=90°. ∴ MC⊥BD. ∴  .
.
(3)连结 ,由
,由 是正方形,知
是正方形,知 ⊥
⊥ .
.
∵  ⊥MC, ∴
⊥MC, ∴  ⊥平面
⊥平面 .
.
∴ 平面 ⊥平面
⊥平面 .
.
(4)∠ 是
是 与平面
与平面 所成的角且等于45°.
所成的角且等于45°.
20.解析:(1) .
.
∵ x≥1. ∴  ,
,
当x≥1时, 是增函数,其最小值为
是增函数,其最小值为 .
.
∴ a<0(a=0时也符合题意). ∴ a≤0.
(2) ,即27
,即27
∴  有极大值点
有极大值点 ,极小值点
,极小值点 .
.
此时f(x)在 ,
, 上时减函数,在
上时减函数,在 ,+
,+ 上是增函数.
上是增函数.
∴ f(x)在 ,
, 上的最小值是
上的最小值是 ,最大值是
,最大值是 ,(因
,(因 ).
).
21.解析:(1)∵ 斜率k存在,不妨设k>0,求出M( ,2).直线MA方程为
,2).直线MA方程为 ,直线MB方程为
,直线MB方程为 .
.
分别与椭圆方程联立,可解出 ,
, .
.
∴  . ∴
. ∴  (定值).
(定值).
(2)设直线AB方程为 ,与
,与 联立,消去y得
联立,消去y得
 .
.
由D>0得-4<m<4,且m≠0,点M到AB的距离为 .
.
设△AMB的面积为S. ∴  .
.
当 时,得
时,得 .
.
22.解析:(1)∵  ,a,
,a, ,
,
∴  ∴
∴  ∴
∴ 
∴  .
.
∴ a=2或a=3(a=3时不合题意,舍去). ∴a=2.
(2) ,
, ,由
,由 可得
可得
 . ∴
. ∴  .
.
∴ b=5
(3)由(2)知 ,
, , ∴
, ∴  .
.
∴  . ∴
. ∴  ,
, .
.
∵  ,
, .
.
当n≥3时,



 .
.
∴  . 综上得
. 综上得 
 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com