某物理兴趣小组应用如图甲所示的装置，将质量为m=1.5kg的钩码P与质量为M=5.0kg的小车Q组成的系统作为研究对象来验证动能定理，其实验步骤如下：（重力加速度g取10m/s²）

       A．将一端带滑轮的木板放在水平桌面上，滑轮的一端伸出桌边沿；

       B．在木板不带滑轮的一端安装打点计时器，用导线将打点计时器跟50Hz交流电源相连；

       C．将小车Q放在木板上打点计时器的附近，纸带穿过打点计时器的限位孔并与小车相连；

       D．细绳的一端与小车Q相连，另一端跨过滑轮与钩码P相连；

       E．接通打点计时器后释放小车Q，打点计时器在纸带上打下一系列点如图乙所示。图中A、B、C……H是计数点，每相邻两个计数点间有4个记录点未标出，设纸带上两个相邻的计数点之间的时间间隔为T。

   （1）纸带上两个相邻的计数点之间的时间间隔T=        S。

   （2）由乙图所示的纸带通过分析计算可知，小车Q运动中受到的阻力f=          。

   （3）从打点计时器打下B点到打下C点的过程中，对钩码P与小车Q组成的系统，合外力做功的公式为W=      （用M、m、g、f、T、S₁、S₂、S₃……中的相关符号表示）；钩码P与小车Q组成系统的动能改变量△E_k=    （用M、m、g、f、T、S₁、S₂、S₃……中的相关符号表示）

   （4）该实验中，每次实验所求得的W都略大于△E_k，引起该实验误差的原因是       （只要答对一个就可得分）

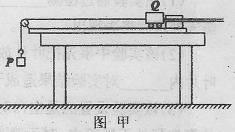
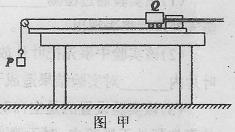
某物理兴趣小组应用如图甲所示的装置，将质量为m=1.5kg的钩码P与质量为M=5.0kg的小车Q组成的系统作为研究对象来验证动能定理，其实验步骤如下：（重力加速度g取10m/s²）

       A．将一端带滑轮的木板放在水平桌面上，滑轮的一端伸出桌边沿；

       B．在木板不带滑轮的一端安装打点计时器，用导线将打点计时器跟50Hz交流电源相连；

       C．将小车Q放在木板上打点计时器的附近，纸带穿过打点计时器的限位孔并与小车相连；

       D．细绳的一端与小车Q相连，另一端跨过滑轮与钩码P相连；

       E．接通打点计时器后释放小车Q，打点计时器在纸带上打下一系列点如图乙所示。图中A、B、C……H是计数点，每相邻两个计数点间有4个记录点未标出，设纸带上两个相邻的计数点之间的时间间隔为T。

   （1）纸带上两个相邻的计数点之间的时间间隔T=        S。

   （2）由乙图所示的纸带通过分析计算可知，小车Q运动中受到的阻力f=          。

   （3）从打点计时器打下B点到打下C点的过程中，对钩码P与小车Q组成的系统，合外力做功的公式为W=      （用M、m、g、f、T、S₁、S₂、S₃……中的相关符号表示）；钩码P与小车Q组成系统的动能改变量△E_k=    （用M、m、g、f、T、S₁、S₂、S₃……中的相关符号表示）

   （4）该实验中，每次实验所求得的W都略大于△E_k，引起该实验误差的原因是       （只要答对一个就可得分）

涡流制动是一种利用电磁感应原理工作的新型制动方式，它的基本原理如图甲所示。水平面上固定一块铝板，当一竖直方向的条形磁铁在铝板上方几毫米高度上水平经过时，铝板内感应出的涡流会对磁铁的运动产生阻碍作用。

涡流制动是磁悬浮列车在高速运行时进行制动的一种方式。某研究所制成如图乙所示的车和轨道模型来定量模拟磁悬浮列车的涡流制动过程。车厢下端安装有电磁铁系统，能在长为，宽的矩形区域内产生竖直方向的匀强磁场，磁感应强度可随车速的减小而自动增大（由车内速度传感器控制），但最大不超过，将铝板简化为长大于，宽也为的单匝矩形线圈，间隔铺设在轨道正中央，其间隔也为，每个线圈的电阻为，导线粗细忽略不计。在某次实验中，模型车速度为时，启动电磁铁系统开始制动，车立即以加速度做匀减速直线运动，当磁感应强度增加到时就保持不变，直到模型车停止运动。已知模型车的总质量为，空气阻力不计。不考虑磁感应强度的变化引起的电磁感应现象以及线圈激发的磁场对电磁铁产生磁场的影响。

（1）电磁铁的磁感应强度达到最大时，模型车的速度为多大？

（2）模型车的制动距离为多大？

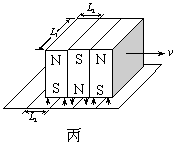
（3）为了节约能源，将电磁铁换成若干个并在一起的永磁铁组，两个相邻的磁铁磁极的极性相反，且将线圈改为连续铺放，如图丙所示，已知模型车质量减为，永磁铁激发的磁感应强度恒为，每个线圈匝数为，电阻为，相邻线圈紧密接触但彼此绝缘。模型车仍以的初速度开始减速，为保证制动距离不大于，至少安装几个永磁铁？

涡流制动是一种利用电磁感应原理工作的新型制动方式，它的基本原理如图甲所示。水平面上固定一块铝板，当一竖直方向的条形磁铁在铝板上方几毫米高度上水平经过时，铝板内感应出的涡流会对磁铁的运动产生阻碍作用。

涡流制动是磁悬浮列车在高速运行时进行制动的一种方式。某研究所制成如图乙所示的车和轨道模型来定量模拟磁悬浮列车的涡流制动过程。车厢下端安装有电磁铁系统，能在长为，宽的矩形区域内产生竖直方向的匀强磁场，磁感应强度可随车速的减小而自动增大（由车内速度传感器控制），但最大不超过，将铝板简化为长大于，宽也为的单匝矩形线圈，间隔铺设在轨道正中央，其间隔也为，每个线圈的电阻为，导线粗细忽略不计。在某次实验中，模型车速度为时，启动电磁铁系统开始制动，车立即以加速度做匀减速直线运动，当磁感应强度增加到时就保持不变，直到模型车停止运动。已知模型车的总质量为，空气阻力不计。不考虑磁感应强度的变化引起的电磁感应现象以及线圈激发的磁场对电磁铁产生磁场的影响。

（1）电磁铁的磁感应强度达到最大时，模型车的速度为多大？

（2）模型车的制动距离为多大？

（3）为了节约能源，将电磁铁换成若干个并在一起的永磁铁组，两个相邻的磁铁磁极的极性相反，且将线圈改为连续铺放，如图丙所示，已知模型车质量减为，永磁铁激发的磁感应强度恒为，每个线圈匝数为，电阻为，相邻线圈紧密接触但彼此绝缘。模型车仍以的初速度开始减速，为保证制动距离不大于，至少安装几个永磁铁？