
题目列表(包括答案和解析)
初中所学角的范围是多少?
| f(x2)-f(x1) |
| x2-x1 |
| f(b)-f(a) |
| b-a |
| b-a |
| b |
| b |
| a |
| b-a |
| a |
如图所示,在Rt△ABC中,∠A、∠B、∠C的对边分别为a、b、c,斜边c是△ABC外接圆的直径(设Rt△ABC外接圆的半径为R),则![]() ,这个结论对钝角三角形、锐角三角形是否也成立呢?你能否结合圆形及初中所学几何知识作出相应的解释?
,这个结论对钝角三角形、锐角三角形是否也成立呢?你能否结合圆形及初中所学几何知识作出相应的解释?

如图所示,OA、OB、OC为不共面的三条射线,点A1、B1、C1分别是OA、OB、OC上的点,且![]() =
=![]() =
=![]() 成立.
成立.
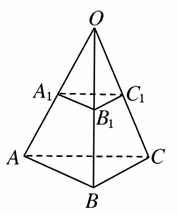
求证:△A1B1C1∽△ABC.
[分析] 由初中所学平面几何知识,可证明两内角对应相等,进而证明两个三角形相似.
试画出所学过的函数的知识结构图.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com