
题目列表(包括答案和解析)
若函数 满足:在定义域内存在实数
满足:在定义域内存在实数 ,使
,使 (k为常数),则称“f(x)关于k可线性分解”.
(k为常数),则称“f(x)关于k可线性分解”.
(Ⅰ)函数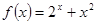 是否关于1可线性分解?请说明理由;
是否关于1可线性分解?请说明理由;
(Ⅱ)已知函数
 关于
关于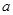 可线性分解,求
可线性分解,求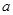 的取值范围;
的取值范围;
(Ⅲ)证明不等式:
 .
.
若函数 满足:集合
满足:集合 中至少存在三个不同的数构成等比数列,则称函数
中至少存在三个不同的数构成等比数列,则称函数 是等比源函数.
是等比源函数.
(Ⅰ)判断下列函数:①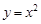 ;②
;② ;③
;③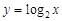 中,哪些是等比源函数?(不需证明)
中,哪些是等比源函数?(不需证明)
(Ⅱ)判断函数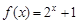 是否为等比源函数,并证明你的结论;
是否为等比源函数,并证明你的结论;
(Ⅲ)证明: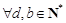 ,函数
,函数 都是等比源函数.
都是等比源函数.
若函数 满足:“对于区间(1,2)上的任意实数
满足:“对于区间(1,2)上的任意实数 ,
,
 恒成立”,则称
恒成立”,则称 为完美函数.给出以下四个函数
为完美函数.给出以下四个函数
① ②
② ③
③ ④
④

其中是完美函数的序号是 .
若函数 满足:“对于区间(1,2)上的任意实数
满足:“对于区间(1,2)上的任意实数 ,
, 恒成立”,则称
恒成立”,则称 为完美函数.给出以下四个函数
为完美函数.给出以下四个函数
① ②
② ③
③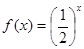 ④
④
其中是完美函数的序号是
若函数 满足:“对于区间(1,2)上的任意实数
满足:“对于区间(1,2)上的任意实数 ,
, 恒成立”,则称
恒成立”,则称 为完美函数.给出以下四个函数
为完美函数.给出以下四个函数
① ②
② ③
③ ④
④
其中是完美函数的是( )
A.① B.② ③ C.①③ D.②③④
一、选择题:D C B B A C A C
二、填空题:9、60 ; 10、8 11、.files/image171.gif) ;12、
;12、.files/image173.gif) 13、
13、.files/image175.gif) ;14、1:6 ; 15、
;14、1:6 ; 15、.files/image177.gif)
三、解答题:
16、解:解: ( 1) 由图知A= 4…………1分 由.files/image179.gif) ,得
,得.files/image181.gif) 所以
所以.files/image183.gif) …3分
…3分
17、解:1)3个旅游团选择3条不同线路的概率为:P1=.files/image200.gif) ……4分
……4分
(2)设选择甲线路旅游团数为ξ,则ξ=0,1,2,3………………5分
P(ξ=0)=.files/image202.gif) P(ξ=1)=
P(ξ=1)=.files/image204.gif) P(ξ=2)=
P(ξ=2)= .files/image206.gif) P(ξ=3)=
P(ξ=3)= .files/image208.gif) …9分
…9分
ξ
0
1
2
3
∴ξ的分布列为:
………………10分
18、(本小题14分)
(1) 因为动圆M,过点F.files/image127.gif) 且与直线
且与直线.files/image129.gif) 相切,所以圆心M到F的距离等于到直线
相切,所以圆心M到F的距离等于到直线.files/image220.gif) 的距离.所以,点M的轨迹是以F为焦点,
的距离.所以,点M的轨迹是以F为焦点, .files/image220.gif) 为准线的抛物线,且
为准线的抛物线,且.files/image222.gif) ,
,.files/image224.gif) ,
所以所求的轨迹方程为
,
所以所求的轨迹方程为.files/image226.gif) ……………5分
……………5分
⑵.解:取AC的中点M,连结OM、ME、OE,由E为BC的中点知.files/image268.gif) ,
,
∴ 直线OE与EM所成的锐角就是异面直线AB与CD所成的角,…………… 8分
∴异面直线AB与CD所成角的余弦值为.files/image281.gif) .
………………………… 11分
.
………………………… 11分
方法二:⑴.同方法一.⑵.解:以O为原点,如图建立空间直角坐标系,则.files/image303.gif)
.files/image313.gif) ,∴
,∴.files/image315.gif) ,令
,令.files/image317.gif) 得
得.files/image319.gif) 是平面ACD的一个法向量.又
是平面ACD的一个法向量.又.files/image321.gif) ∴点E到平面ACD的距离
∴点E到平面ACD的距离 .files/image323.gif) .…14分
.…14分
此时.files/image054.gif) 无最小值. ……10分 ②当
无最小值. ……10分 ②当.files/image379.gif) 时,
时,.files/image054.gif) 在
在.files/image382.gif) 上单调递减,在
上单调递减,在.files/image384.gif) 上单调递增
上单调递增
③ 当.files/image390.gif) 时,
时,.files/image054.gif) 在
在.files/image342.gif) 上单调递减,
上单调递减,.files/image375.gif) ,
,.files/image377.gif) (舍去),所以,此时
(舍去),所以,此时.files/image054.gif) 无最小值.综上,存在实数
无最小值.综上,存在实数.files/image388.gif) ,使得当
,使得当.files/image365.gif) 时
时.files/image054.gif) 有最小值3.
有最小值3.
本资料由《七彩教育网》www.7caiedu.cn 提供!
本资料来源于《七彩教育网》http://www.7caiedu.cn
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com