
题目列表(包括答案和解析)
(本小题满分14分)
如图6所示,等腰三角形△ABC的底边AB=![]() ,高CD=3.点E是线段BD上异于B、D的动点.点F在BC边上,且EF⊥AB.现沿EF将△BEF折起到△PEF的位置,使PE⊥AE.
,高CD=3.点E是线段BD上异于B、D的动点.点F在BC边上,且EF⊥AB.现沿EF将△BEF折起到△PEF的位置,使PE⊥AE.
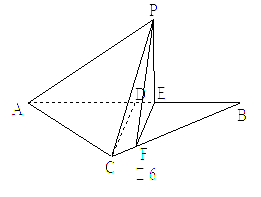 记BE=x,V(x)表示四棱锥P-ACFE的体积。
记BE=x,V(x)表示四棱锥P-ACFE的体积。
(1)求V(x)的表达式;
(2)当x为何值时,V(x)取得最大值?
(3)当V(x)取得最大值时,求异面直线
AC与PF所成角的余弦值。
(本小题满分14分)
如图5所示,四棱锥![]() 的底面
的底面![]() 是半径为
是半径为![]() 的圆的内接四边形,其中
的圆的内接四边形,其中![]() 是圆的直径,
是圆的直径,![]() ,
,![]() ,
,![]() .
.
(1)求线段![]() 的长;
的长;
(2)若![]() ,求三棱锥
,求三棱锥![]() 的体积.
的体积.
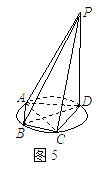
(本小题满分14分)
如图5所示,在三棱锥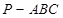 中,
中,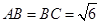 ,平面
,平面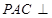 平面
平面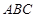 ,
,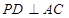 于点
于点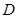 ,
,
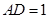 ,
,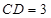 ,
,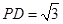 .
.
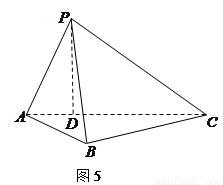
(1)证明△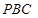 为直角三角形;
为直角三角形;
(2)求直线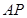 与平面
与平面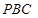 所成角的正弦值
所成角的正弦值
(本小题满分14分)
如图6所示,等腰三角形△ABC的底边AB=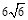 ,高CD=3.点E是线段BD上异于B、D的动点.点F在BC边上,且EF⊥AB.现沿EF将△BEF折起到△PEF的位置,使PE⊥AE.
,高CD=3.点E是线段BD上异于B、D的动点.点F在BC边上,且EF⊥AB.现沿EF将△BEF折起到△PEF的位置,使PE⊥AE.
记BE=x,V(x)表示四棱锥P-ACFE的体积。
(1)求V(x)的表达式;
(2)当x为何值时,V(x)取得最大值?
(3)当V(x)取得最大值时,求异面直线
AC与PF所成角的余弦值。
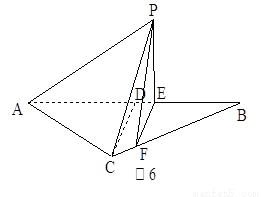
(本小题满分14分)
如图6所示,等腰三角形△ABC的底边AB=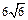 ,高CD=3.点E是线段BD上异于B、D的动点.点F在BC边上,且EF⊥AB.现沿EF将△BEF折起到△PEF的位置,使PE⊥AE.
,高CD=3.点E是线段BD上异于B、D的动点.点F在BC边上,且EF⊥AB.现沿EF将△BEF折起到△PEF的位置,使PE⊥AE.
记BE=x,V(x)表示四棱锥P-ACFE的体积。
(1)求V(x)的表达式;
(2)当x为何值时,V(x)取得最大值?
(3)当V(x)取得最大值时,求异面直线
AC与PF所成角的余弦值。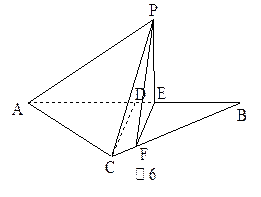
一、 选择题: ACAAD;CBDBC
二、 填空题:
三、解答题:
16.解:
17.解:
(-2,-2),(-2,0),(-2,1),(-2,3);(0,-2),(0,0),(0,1),(0,3);
(1,-2),(1,0),(1,1),(1,3);(3,-2),(3,0),(3,1),(3,3)…………………….4分
(2)点M不在x轴上的坐标共有12种:
(-2,-2),(-2,0),(-2,1),(-2,3);(1,-2),(1,0),(1,1),(1,3);
(3,-2),(3,0),(3,1),(3,3)
所以点M不在x轴上的概率是.files/image174.gif) ………………………………………..8分
………………………………………..8分
(3)点M正好落在区域.files/image129.gif) 上的坐标共有3种:(1,1),(1,3),(3,1)
上的坐标共有3种:(1,1),(1,3),(3,1)
故M正好落在该区域上的概率为.files/image176.gif) …………………………………………………12分
…………………………………………………12分
18、解:
(1)判断:AB//平面DEF………………………………………………..2分
AC,BC的中点,有
EF//AB………………..5分
又因
所以
AB//平面DEF……………..7分
故EM.files/image133.gif) 平面BCD 于是EM是三棱锥E-CDF的高……………………………..9分
平面BCD 于是EM是三棱锥E-CDF的高……………………………..9分
EM=.files/image192.gif) ……………………………………………………………………11分
……………………………………………………………………11分
故三棱锥C-DEF的体积为
19、解:
所以所求的椭圆的方程是:.files/image204.gif) ………………………………………….6分
………………………………………….6分
.files/image210.gif) 在C内,故过
在C内,故过.files/image210.gif) 没有圆C的切线……………………………………………….8分
没有圆C的切线……………………………………………….8分
20、解:
2
(2)1
2
21.解:
当n为偶数时,
当n为奇数时,
当n为奇数时,
当n为偶数时,
本资料由《七彩教育网》www.7caiedu.cn 提供!
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com