
题目列表(包括答案和解析)



 的通项公式;
的通项公式; ,若
,若 对
对 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围; 为首项,公比为
为首项,公比为 的数列
的数列 ,
, ,使得数列
,使得数列 中每一项都是数列
中每一项都是数列 中不同的项,若存在,求出所有满足条件的数列
中不同的项,若存在,求出所有满足条件的数列 的通项公式;若不存在,说明理由
的通项公式;若不存在,说明理由数列![]() 的通项公式
的通项公式![]()
![]()
(1)求:f(1)、f(2)、f(3)、f(4)的值;
(2)由上述结果推测出计算f(n)的公式,并用数学归纳法加以证明.
设数列![]() 的通项公式为
的通项公式为![]() 。数列
。数列![]() 定义如下:对于正整数m,
定义如下:对于正整数m,![]() 是使得不等式
是使得不等式![]() 成立的所有n中的最小值。 (1)若
成立的所有n中的最小值。 (1)若![]() ,求b3; (2)若
,求b3; (2)若![]() ,求数列
,求数列![]() 的前2m项和公式;(3)是否存在p和q,使得
的前2m项和公式;(3)是否存在p和q,使得![]() ?如果存在,求p和q的取值范围;如果不存在,请说明理由。
?如果存在,求p和q的取值范围;如果不存在,请说明理由。
设数列![]() 的通项公式为
的通项公式为![]() 。数列
。数列![]() 定义如下:对于正整数m,
定义如下:对于正整数m,![]() 是使得不等式
是使得不等式![]() 成立的所有n中的最小值。
成立的所有n中的最小值。
(1)若![]() ,求b3;
,求b3;
(2)若![]() ,求数列
,求数列![]() 的前2m项和公式;
的前2m项和公式;
(3)是否存在p和q,使得![]() ?如果存在,求p和q的取值范围;如果不存在,请说明理由。
?如果存在,求p和q的取值范围;如果不存在,请说明理由。
设数列 的通项公式为
的通项公式为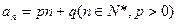 。数列
。数列 定义如下:对于正整数m,
定义如下:对于正整数m, 是使得不等式
是使得不等式 成立的所有n中的最小值。 (1)若
成立的所有n中的最小值。 (1)若 ,求b3; (2)若
,求b3; (2)若 ,求数列
,求数列 的前2m项和公式;(3)是否存在p和q,使得
的前2m项和公式;(3)是否存在p和q,使得 ?如果存在,求p和q的取值范围;如果不存在,请说明理由。
?如果存在,求p和q的取值范围;如果不存在,请说明理由。
一、 选择题: ACAAD;CBDBC
二、 填空题:
三、解答题:
16.解:
17.解:
(-2,-2),(-2,0),(-2,1),(-2,3);(0,-2),(0,0),(0,1),(0,3);
(1,-2),(1,0),(1,1),(1,3);(3,-2),(3,0),(3,1),(3,3)…………………….4分
(2)点M不在x轴上的坐标共有12种:
(-2,-2),(-2,0),(-2,1),(-2,3);(1,-2),(1,0),(1,1),(1,3);
(3,-2),(3,0),(3,1),(3,3)
所以点M不在x轴上的概率是.files/image174.gif) ………………………………………..8分
………………………………………..8分
(3)点M正好落在区域.files/image129.gif) 上的坐标共有3种:(1,1),(1,3),(3,1)
上的坐标共有3种:(1,1),(1,3),(3,1)
故M正好落在该区域上的概率为.files/image176.gif) …………………………………………………12分
…………………………………………………12分
18、解:
(1)判断:AB//平面DEF………………………………………………..2分
AC,BC的中点,有
EF//AB………………..5分
又因
所以
AB//平面DEF……………..7分
故EM.files/image133.gif) 平面BCD 于是EM是三棱锥E-CDF的高……………………………..9分
平面BCD 于是EM是三棱锥E-CDF的高……………………………..9分
EM=.files/image192.gif) ……………………………………………………………………11分
……………………………………………………………………11分
故三棱锥C-DEF的体积为
19、解:
所以所求的椭圆的方程是:.files/image204.gif) ………………………………………….6分
………………………………………….6分
.files/image210.gif) 在C内,故过
在C内,故过.files/image210.gif) 没有圆C的切线……………………………………………….8分
没有圆C的切线……………………………………………….8分
20、解:
2
(2)1
2
21.解:
当n为偶数时,
当n为奇数时,
当n为奇数时,
当n为偶数时,
本资料由《七彩教育网》www.7caiedu.cn 提供!
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com