(3)设cn= Sn+nan.Tn为数列{cn}的前n项和.求证:Tn<1. 【
查看更多】
题目列表(包括答案和解析)
数列{a
n}的前n项和为S
n,首项a
1=a,且
an+1=2Sn+1,n∈N*(1)若数列{a
n}是等比数列,求实数a的值;
(2)设b
n=na
n,在(1)的条件下,求数列{b
n}的前n项和T
n;
(3)设各项不为0的数列{c
n}中,所有满足c
i•c
i+1<0的整数i的个数称为这个数列{c
n}的“积异号数”,令
cn=(n∈N*),在(2)的条件下,求数列{c
n}的“积异号数”.
查看答案和解析>>
数列{an}的前n项和记为Sn,a1=t,点(Sn,an+1)在直线y=2x+1上,n∈N*.
(1)若数列{an}是等比数列,求实数t的值;
(2)设bn=nan,在(1)的条件下,求数列{bn}的前n项和Tn;
(3)设各项均不为0的数列{cn}中,所有满足ci•ci+1<0的整数i的个数称为这个数列{cn}的“积异号数”,令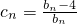 (n∈N*),在(2)的条件下,求数列{cn}的“积异号数”.
(n∈N*),在(2)的条件下,求数列{cn}的“积异号数”.
查看答案和解析>>
数列{a
n}的前n项和记为S
n,a
1=t,点(S
n,a
n+1)在直线y=2x+1上,n∈N
*.
(1)若数列{a
n}是等比数列,求实数t的值;
(2)设b
n=na
n,在(1)的条件下,求数列{b
n}的前n项和T
n;
(3)设各项均不为0的数列{c
n}中,所有满足c
i•c
i+1<0的整数i的个数称为这个数列{c
n}的“积异号数”,令
cn=(n∈N
*),在(2)的条件下,求数列{c
n}的“积异号数”.
查看答案和解析>>
数列{a
n}的前n项和为S
n,首项a
1=a,且
an+1=2Sn+1,n∈N*(1)若数列{a
n}是等比数列,求实数a的值;
(2)设b
n=na
n,在(1)的条件下,求数列{b
n}的前n项和T
n;
(3)设各项不为0的数列{c
n}中,所有满足c
i•c
i+1<0的整数i的个数称为这个数列{c
n}的“积异号数”,令
cn=(n∈N*),在(2)的条件下,求数列{c
n}的“积异号数”.
查看答案和解析>>
数列{a
n}的前n项和记为S
n,a
1=t,点

在直线y=2x+1上,

。
(1)若数列{a
n}是等比数列,求实数t的值;
(2)设b
n=na
n,在(1)的条件下,求数列{b
n}的前n项和T
n;
(3)设各项均不为0的数列{c
n}中,所有满足
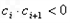
的整数

的个数称为这个数列

的”,令

(

),在(2)的条件下,求数列

的“积异号数”。
查看答案和解析>>

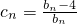 (n∈N*),在(2)的条件下,求数列{cn}的“积异号数”.
(n∈N*),在(2)的条件下,求数列{cn}的“积异号数”. 在直线y=2x+1上,
在直线y=2x+1上, 。
。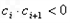 的整数
的整数 的个数称为这个数列
的个数称为这个数列 的”,令
的”,令 (
( ),在(2)的条件下,求数列
),在(2)的条件下,求数列 的“积异号数”。
的“积异号数”。