
题目列表(包括答案和解析)
(本小题满分12分)
某中学研究性学习小组,为了考察高中学生的作文水平与爱看课外书的关系,在本校高三年级随机调查了 50名学生.调査结果表明:在爱看课外书的25人中有18人作文水平好,另7人作文水平一般;在不爱看课外书的25人中有6人作文水平好,另19人作文水平一般.
(Ⅰ)试根据以上数据完成以下2×2列联表,并运用独立性检验思想,指出有多大把握认为中学生的作文水平与爱看课外书有关系?
高中学生的作文水平与爱看课外书的2×2列联表
|
|
爱看课外书 |
不爱看课外书 |
总计 |
|
作文水平好 |
|
|
|
|
作文水平一般 |
[来源:学。科。网Z。X。X。K] |
|
|
|
总计 |
|
|
|
(Ⅱ)将其中某5名爱看课外书且作文水平好的学生分别编号为1、2、3、4、5,某5名爱看课外书且作文水平一般的学生也分别编号为1、2、3、4、5,从这两组学生中各任选1人进行学习交流,求被选取的两名学生的编号之和为3的倍数或4的倍数的概率.
参考公式: ,其中
,其中 .
.
参考数据:
|
|
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
|
|
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
(本小题满分12分)
某中学研究性学习小组,为了考察高中学生的作文水平与爱看课外书的关系,在本校高三年级随机调查了 50名学生.调査结果表明:在爱看课外书的25人中有18人作文水平好,另7人作文水平一般;在不爱看课外书的25人中有6人作文水平好,另19人作文水平一般.
(Ⅰ)试根据以上数据完成以下2×2列联表,并运用独 立性检验思想,指出有多大把握认为中学生的作文水平与爱看课外书有关系?
立性检验思想,指出有多大把握认为中学生的作文水平与爱看课外书有关系?
高中学生的作文水平与爱看课外书的2×2列联表
| | 爱看课外书 | 不爱看课外书 | 总计 |
作文水平 好 好 | | | |
| 作文水平一般 | [来源:学。科。网Z。X。X。K] | | |
| 总计 | | | |
 分别编号为1、2、3、4、5,从这两组学生中各任选1人进行学习交流,求被选取的两名学生的编号之和为3的倍数或4的倍数的概率.
分别编号为1、2、3、4、5,从这两组学生中各任选1人进行学习交流,求被选取的两名学生的编号之和为3的倍数或4的倍数的概率.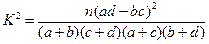 ,其中
,其中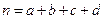 .
.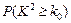 [来源:学*科*网] [来源:学*科*网] | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
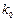 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
一.选择题:DCBBA
二.填空题:11.4x-3y-17 = 0 12.33 13. 14.
14. 15.
15.
三.解答题:
16.(1)解:由频率分布条形图知,抽取的学生总数为 人 4分
人 4分
∵各班被抽取的学生人数成等差数列,设其公差为d
由4×22+6d = 100解得:d = 2 6分
∴各班被抽取的学生人数分别是22人,24人,26人,28人. 8分
(2)解:在抽取的学生中,任取一名学生,分数不小于90分的概率为
0.35+0.25+0.1+0.05=0.75 12分
17.(1)解:∵ ,
, 2分
2分
∴由 得:
得: ,即
,即 4分
4分
又∵ ,∴
,∴ 6分
6分
(2)解: 8分
8分
由 得:
得: ,即
,即 10分
10分
两边平方得: ,∴
,∴ 12分
12分
18.方法一
 (1)证:∵CD⊥AB,CD⊥BC,∴CD⊥平面ABC 2分
(1)证:∵CD⊥AB,CD⊥BC,∴CD⊥平面ABC 2分
又∵CDÌ平面ACD,∴平面ACD⊥平面ABC 4分
(2)解:∵AB⊥BC,AB⊥CD,∴AB⊥平面BCD,故AB⊥BD
∴∠CBD是二面角C-AB-D的平面角
6分
∵在Rt△BCD中,BC = CD,∴∠CBD = 45°
即二面角C-AB-D的大小为45°
8分
(3)解:过点B作BH⊥AC,垂足为H,连结DH
∵平面ACD⊥平面ABC,∴BH⊥平面ACD,
∴∠BDH为BD与平面ACD所成的角
10分
设AB = a,在Rt△BHD中, ,
,
∴ , 10分
, 10分
解得: ,即线段AB的长度为1 12分
,即线段AB的长度为1 12分
 方法二
方法二
(1)同方法一 4分
(2)解:设以过B点且∥CD的向量为x轴, 为y轴和z轴建立如图所示的空间直角坐标系,设AB = a,则A(0,0,a),C(0,1,0),D(1,1,0),
为y轴和z轴建立如图所示的空间直角坐标系,设AB = a,则A(0,0,a),C(0,1,0),D(1,1,0), = (1,1,0),
= (1,1,0), = (0,0,a)
= (0,0,a)
平面ABC的法向量 = (1,0,0)
= (1,0,0)
设平面ABD的一个法向量为n = (x,y,z),则

取n = (1,-1,0)
6分

∴二面角C-AB-D的大小为45° 8分
(3)解: = (0,1,-a),
= (0,1,-a), = (1,0,0),
= (1,0,0), = (1,1,0)
= (1,1,0)
设平面ACD的一个法向量是m = (x,y,z),则
∴取m = (0,a,1),由直线BD与平面ACD所成角为30°,故向量 、m的夹角为60°
、m的夹角为60°
故 10分
10分
解得: ,即线段AB的长度为1 12分
,即线段AB的长度为1 12分
19.(1)解:设M (x,y),在△MAB中,| AB | = 2,
∴
即 2分
2分
因此点M的轨迹是以A、B为焦点的椭圆,a = 2,c = 1
∴曲线C的方程为 . 4分
. 4分
(2)解法一:设直线PQ方程为 (
( ∈R)
∈R)
由 得:
得: 6分
6分
显然,方程①的 ,设P(x1,y1),Q(x2,y2),则有
,设P(x1,y1),Q(x2,y2),则有

 8分
8分
令 ,则t≥4,
,则t≥4, 10分
10分
当 时有最大值9,故
时有最大值9,故 ,即S≤3,∴△APQ的最大值为3 12分
,即S≤3,∴△APQ的最大值为3 12分
解法二:设P(x1,y1),Q(x2,y2),则
当直线PQ的斜率不存在时,易知S = 3
设直线PQ方程为
由 得:
得: ① 6分
① 6分
显然,方程①的△>0,则
∴ 8分
8分
 10分
10分
令 ,则
,则
∴ ,即S<3
,即S<3
∴△APQ的最大值为3 12分
20.(1)解:
∵a<0,∴
故函数f (x)在区间(-∞, )、(-a,+∞)上单调递增,在(
)、(-a,+∞)上单调递增,在( ,-a)上单调递减 4分
,-a)上单调递减 4分
(2)解:∵二次函数 有最大值,∴a<0 5分
有最大值,∴a<0 5分
由 得:
得: 6分
6分
∵函数 与
与 的图象只有一个公共点,
的图象只有一个公共点,
∴ ,又a<0,∴-1≤a<0 8分
,又a<0,∴-1≤a<0 8分
又 ,∴
,∴ (-1≤a<0) 10分
(-1≤a<0) 10分
(3)解:当a < 0时,函数f (x)在区间(-∞, )、(-a,+∞)上单调递增,
)、(-a,+∞)上单调递增,
函数g (x)在区间(-∞, )上单调递增
)上单调递增
∴ 12分
12分
当a > 0时,函数f (x)在区间(-∞,-a)、( ,+∞)上单调递增,
,+∞)上单调递增,
函数g (x)在区间( ,+∞)上单调递增
,+∞)上单调递增
∴
综上所述,实数a的取值范围是(-∞, ]∪[3,+∞) 13分
]∪[3,+∞) 13分
21.(1)解:记
令x = 1得:
令x =-1得:
两式相减得: ,∴
,∴ 4分
4分
当n≥2时,
当n = 1时, ,适合上式
,适合上式
∴ 6分
6分
(2)解:
注意到 8分
8分
 可改写为:
可改写为:

∴
故 10分
10分
∴
 12分
12分
 14分
14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com