
题目列表(包括答案和解析)
| ||
|
|
|
| ||
|
|
| OA |
| OB |
| OM |
| OA |
| OB |
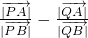 的值.
的值.一. 每小题5分,共60分 DACDB DACBB DD
二. 每小题5分,共20分.其中第16题前空2分,后空3分.
13.
60;
14.  ; 15.
; 15.  ; 16. 2,-
; 16. 2,-
三.解答题:本大题共6个小题,共70分.解答应写出文字说明,证明过程或演算步骤.
17.(Ⅰ)
∴


(Ⅱ) (7分)
(7分)
 (8分)
(8分)
∴ (10分)
(10分)
18.解:(Ⅰ)记“该人被录用”的事件为事件A,其对立事件为 ,则
,则


(Ⅱ)该生参加测试次数ξ的可能取值为2,3,4,依题意得
|