
题目列表(包括答案和解析)
在圆中有结论![]() :如图,“AB是圆O的直径,直线AC,BD是圆O过A,B的切线,P是圆
:如图,“AB是圆O的直径,直线AC,BD是圆O过A,B的切线,P是圆![]() O上任意一点,CD是过P的切线,则有PO2=PC·PD”.类比到椭圆:“AB是椭圆的长轴,直线AC,BD是椭圆过A
O上任意一点,CD是过P的切线,则有PO2=PC·PD”.类比到椭圆:“AB是椭圆的长轴,直线AC,BD是椭圆过A![]() ,B的切线,P是椭圆上任意一点,CD是过P的切线,则有______.”
,B的切线,P是椭圆上任意一点,CD是过P的切线,则有______.”
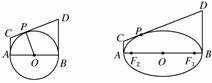
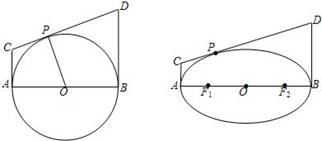
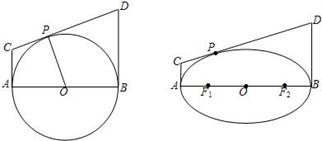
在圆中有结论:如图所示,“AB是圆O的直径,直线AC,BD是圆O过A,B的切线,P是圆O上任意一点,CD是过P的切线,则有PO2=PC·PD”.类比到椭圆:“AB是椭圆的长轴,直线AC,BD是椭圆过A,B的切线,P是椭圆上任意一点,CD是过P的切线,则有__▲__.”
 、
、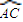 的中点,给出下列结论:
的中点,给出下列结论: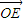 在向量
在向量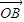 方向上的投影恰为
方向上的投影恰为 ;
;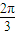 ;
; 的中点,则过点M且与直线EF、PC成等角的直线只有三条,其中正确的是( )
的中点,则过点M且与直线EF、PC成等角的直线只有三条,其中正确的是( )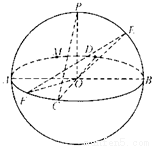
 、
、 的中点,给出下列结论:
的中点,给出下列结论: ;
; 在向量
在向量 方向上的投影恰为
方向上的投影恰为 ;
; 的中点,则过点M且与直线EF、PC成等角的直线有无数条;
的中点,则过点M且与直线EF、PC成等角的直线有无数条;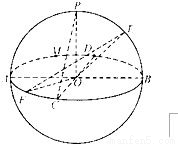
一、选择题
题号
1
2
3
4
5
6
7
8
9
10
答案
A
D
A
A
A
A
B
B
A
D
二、填空题
11. 8 + ; 12. 60; 13..files/image055.gif) ; 14. 14; 15.
; 14. 14; 15. .files/image213.gif) .
.
三、解答题
16. 解:(1)依题意的.files/image215.gif) ,所以
,所以.files/image217.gif) ,于是
,于是.files/image219.gif) ……………2分
……………2分
由.files/image221.gif) 解得
解得.files/image223.gif) ……………4分
……………4分
把.files/image225.gif) 代入
代入.files/image227.gif) ,可得
,可得.files/image229.gif) ,所以
,所以.files/image231.gif) ,
,
所以.files/image233.gif) ,因为
,因为.files/image235.gif) ,所以
,所以.files/image237.gif) 综上所述,
综上所述,.files/image239.gif) …………7分
…………7分
(2)令.files/image241.gif) ,得
,得.files/image243.gif) ,又
,又.files/image245.gif)
.files/image135.gif)
.files/image248.gif)
.files/image250.gif) 故
故.files/image252.gif) 函数
函数.files/image133.gif) 的零点是
的零点是.files/image252.gif) ……………10分
……………10分
.files/image255.gif)
.files/image257.gif) 由
由.files/image259.gif) 得
得.files/image261.gif)
.files/image257.gif) 函数
函数.files/image133.gif) 的单调递增区间是
的单调递增区间是.files/image263.gif) ……………13分
……………13分
17. 解:(1)当.files/image150.gif) 为
为.files/image152.gif) 中点时,有
中点时,有.files/image155.gif) 平面
平面.files/image157.gif) ………2分
………2分
.files/image264.gif) 证明:连结
证明:连结.files/image266.gif) 交
交.files/image268.gif) 于
于.files/image270.gif) ,连结
,连结.files/image272.gif) ∵四边形
∵四边形.files/image146.gif) 是矩形 ∴
是矩形 ∴.files/image270.gif) 为
为.files/image266.gif) 中点
中点
又.files/image150.gif) 为
为.files/image152.gif) 中点,从而
中点,从而.files/image274.gif) ……………………………4分
……………………………4分
∵.files/image276.gif) 平面
平面.files/image157.gif) ,
,.files/image278.gif) 平面
平面.files/image157.gif) ∴
∴.files/image155.gif) 平面
平面.files/image157.gif) ……………6分
……………6分
(2)建立空间直角坐标系.files/image280.gif) 如图所示,则
如图所示,则.files/image282.gif) ,
,.files/image284.gif) ,
,.files/image286.gif) ,
,.files/image288.gif) ,
,.files/image290.gif) ……7分
……7分
所以.files/image292.gif) ,
,.files/image294.gif) . ……………………………8分
. ……………………………8分
设.files/image296.gif) 为平面
为平面.files/image157.gif) 的法向量,则有
的法向量,则有.files/image298.gif) ,即
,即.files/image300.gif) 令
令.files/image302.gif) ,可得平面
,可得平面.files/image157.gif) 的一个法向量为
的一个法向量为.files/image304.gif) ,
,
而平面.files/image306.gif) 的一个法向量为
的一个法向量为.files/image308.gif) ……………11分
……………11分
所以.files/image310.gif) 所以二面角
所以二面角.files/image160.gif) 的余弦值为
的余弦值为.files/image312.gif) ……………13分
……………13分
18. 解:
19.解:
(1)依题意双曲线方程可化为.files/image314.gif) 则
则.files/image316.gif)
.files/image257.gif)
.files/image166.gif) =4
=4.files/image319.gif)
.files/image316.gif)
.files/image257.gif) 点P的轨迹是以
点P的轨迹是以.files/image322.gif) 为焦点的椭圆,其方程可设为
为焦点的椭圆,其方程可设为.files/image324.gif)
.files/image257.gif) 由
由.files/image326.gif) 得
得.files/image328.gif)
.files/image330.gif) 则所求椭圆方程为
则所求椭圆方程为.files/image332.gif) ,
,
故动点P的轨迹E的方程为.files/image332.gif) ;………………3分
;………………3分
(2)设.files/image334.gif) ,
,.files/image336.gif) 则由
则由.files/image338.gif) ,
,.files/image316.gif) 可知
可知
在.files/image340.gif) 中
中.files/image342.gif)
又.files/image344.gif)
.files/image346.gif) 即
即.files/image348.gif)
.files/image350.gif)
当且仅当.files/image352.gif) 时等号成立.故
时等号成立.故.files/image168.gif) 的最小值为
的最小值为.files/image354.gif) ………………6分
………………6分
(3)当.files/image071.gif) 与
与.files/image040.gif) 轴重合时,构不成角AMB,不合题意.
轴重合时,构不成角AMB,不合题意.
当.files/image358.gif) 轴时,直线
轴时,直线.files/image071.gif) 的方程为
的方程为.files/image361.gif) ,代入
,代入.files/image363.gif) 解得
解得.files/image188.gif) 、
、.files/image366.gif) 的坐标分别为
的坐标分别为.files/image368.gif) 、
、.files/image370.gif) 而
而.files/image372.gif) ,∴
,∴.files/image374.gif) ,猜测
,猜测.files/image374.gif) 为定值.………8分
为定值.………8分
证明:设直线.files/image071.gif) 的方程为
的方程为.files/image376.gif) ,由
,由
.files/image378.gif) ,得
,得.files/image380.gif)
∴.files/image382.gif) ,
,.files/image384.gif) ………10分
………10分
∴.files/image386.gif)
.files/image388.gif)
.files/image390.gif)
.files/image392.gif)
.files/image394.gif)
.files/image396.gif)
∴ .files/image374.gif) 为定值。(AB与点M不重合) ……13分
为定值。(AB与点M不重合) ……13分
20.解:
(1)当.files/image398.gif) 时,由
时,由.files/image400.gif) 得
得.files/image402.gif) ;当
;当.files/image404.gif) 时由
时由.files/image406.gif) 得
得.files/image408.gif)
综上:当.files/image398.gif) 时函数
时函数.files/image133.gif) 的定义域为
的定义域为.files/image008.gif) ;
当
;
当.files/image404.gif) 时函数
时函数.files/image133.gif) 的定义域为
的定义域为.files/image411.gif) ………3分
………3分
(2).files/image413.gif)
.files/image415.gif) ………5分
………5分
令.files/image417.gif) 时,得
时,得.files/image419.gif) 即
即.files/image421.gif) ,
,
①当.files/image423.gif) 时,
时,.files/image425.gif) 时
时.files/image427.gif) ,当
,当.files/image429.gif) 时,
时,.files/image431.gif) ,
,
故当.files/image423.gif) 时,函数的递增区间为
时,函数的递增区间为.files/image433.gif) ,递减区间为
,递减区间为.files/image435.gif)
②当.files/image437.gif) 时,
时,.files/image439.gif) ,所以
,所以.files/image427.gif) ,
,
故当.files/image437.gif) 时,
时,.files/image133.gif) 在
在.files/image443.gif) 上单调递增.
上单调递增.
③当.files/image445.gif) 时,若
时,若.files/image447.gif) ,
,.files/image431.gif) ;若
;若.files/image450.gif) ,
,.files/image427.gif) ,
,
故当.files/image445.gif) 时,
时,.files/image133.gif) 的单调递增区间为
的单调递增区间为.files/image452.gif) ;单调递减区间为
;单调递减区间为.files/image454.gif) .
.
综上:当.files/image423.gif) 时,
时,.files/image133.gif) 的单调递增区间为
的单调递增区间为.files/image433.gif) ;单调递减区间为
;单调递减区间为.files/image435.gif)
当.files/image437.gif) 时,
时,.files/image133.gif) 的单调递增区间为
的单调递增区间为.files/image456.gif) ;
;
当.files/image445.gif) 时,
时,.files/image133.gif) 的单调递增区间为
的单调递增区间为.files/image452.gif) ;单调递减区间为
;单调递减区间为.files/image454.gif) ; …10分
; …10分
(Ⅲ)因为当.files/image423.gif) 时,函数的递增区间为
时,函数的递增区间为.files/image433.gif) ;单调递减区间为
;单调递减区间为.files/image435.gif)
若存在.files/image040.gif) 使得
使得.files/image183.gif) 成立,只须
成立,只须.files/image460.gif) ,
,
即.files/image462.gif) ………14分
………14分
21.(本题满分14分,共3小题,任选其中2题作答,每小题7分)
(1)选修4-2:矩阵与变换
解:由 M=.files/image192.gif)
.files/image194.gif) N=
N=.files/image198.gif)
.files/image200.gif) 可得
可得.files/image464.gif)
.files/image466.gif) 的特征多项式为
的特征多项式为.files/image468.gif)
令.files/image470.gif) 得矩阵
得矩阵.files/image188.gif) 的特征值为
的特征值为.files/image472.gif)
再分别求得对应于特征值.files/image474.gif) 的特征向量
的特征向量.files/image476.gif) …………7分
…………7分
.files/image477.gif) (2) 选修4-5:不等式选讲
(2) 选修4-5:不等式选讲
(1)解:依题意可知.files/image479.gif) ,
,
则函数.files/image204.gif) 的图像如图所示:
的图像如图所示:
(2)由函数.files/image204.gif) 的图像容易求得原不等式的解集为
的图像容易求得原不等式的解集为.files/image481.gif) …………7分
…………7分
(3) 选修4-4:坐标系与参数方程
解:由
.files/image208.gif) 即
即.files/image483.gif) 则易得
则易得.files/image485.gif) 由
由.files/image210.gif) 易得
易得.files/image487.gif)
.files/image257.gif) 圆心
圆心.files/image490.gif) 到直线的距离为
到直线的距离为.files/image492.gif)
.files/image245.gif) 又圆的半径为2 ,
又圆的半径为2 , .files/image257.gif) 圆上的点到直线的距离的最小值为
圆上的点到直线的距离的最小值为.files/image495.gif) …………7分
…………7分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com