
题目列表(包括答案和解析)
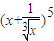 的展开式的各项中任取一项,若其系数为奇数时得2分,其系数为偶数时得0分,现从中随机取一项,则其得分的数学期望值是 .
的展开式的各项中任取一项,若其系数为奇数时得2分,其系数为偶数时得0分,现从中随机取一项,则其得分的数学期望值是 .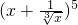 的展开式的各项中任取一项,若其系数为奇数时得2分,其系数为偶数时得0分,现从中随机取一项,则其得分的数学期望值是________.
的展开式的各项中任取一项,若其系数为奇数时得2分,其系数为偶数时得0分,现从中随机取一项,则其得分的数学期望值是________.| 3 | x |
| x |
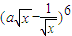 的展开式中的常数项为-160,则
的展开式中的常数项为-160,则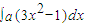 = .
= .| 月 份x | 1 | 2 | 3 | 4 |
| 用水量y | 4.5 | 4 | 3 | 2.5 |
| x |
| 1 | ||
|
| ∫ | a 0 |
| 月 份x | 1 | 2 | 3 | 4 |
| 用水量y | 4.5 | 4 | 3 | 2.5 |
一、1、D 2、A 3、B 4、D 5、B 6、C 7、A 8、D 9、A 10、C
二、11、二 12、2cm 13、1 14、49720, 15、5www.ks5 u.com
三、16、解:
(1).files/image242.gif) ……3分
……3分
.files/image244.gif) ,得
,得.files/image246.gif) ……………………………5分
……………………………5分
(2)由(1)得.files/image248.gif) ………7分
………7分
.files/image250.gif) 当
当.files/image252.gif) 时,
时,.files/image228.gif) 的最大值为
的最大值为.files/image255.gif) …………………………………9分
…………………………………9分
由.files/image252.gif) ,得
,得.files/image150.gif) 值为集合为
值为集合为.files/image259.gif) ………………………10分
………………………10分
(3)由.files/image261.gif) 得
得.files/image263.gif) 所以
所以.files/image265.gif) 时,
时,.files/image048.gif) 为所求….12分
为所求….12分
17、解:www.ks5 u.com
(1).files/image268.gif)
.files/image270.gif) 数列
数列.files/image127.gif) 的各项均为正数,
的各项均为正数,.files/image273.gif)
即.files/image275.gif) ,所以数列
,所以数列.files/image127.gif) 是以2为公比的等比数列……………………3分
是以2为公比的等比数列……………………3分
.files/image277.gif) 是
是.files/image279.gif) 的等差中项,
的等差中项,.files/image281.gif)
.files/image250.gif) 数列
数列.files/image127.gif) 的通项公式
的通项公式.files/image284.gif) …………………………………………………………6分
…………………………………………………………6分
(2)由(1)及.files/image177.gif) 得
得.files/image287.gif) ,…………………………………………8分
,…………………………………………8分
.files/image289.gif)
.files/image291.gif) ①
①
.files/image293.gif) ②
②
②-①得,
.files/image295.gif) …10分
…10分
要使.files/image181.gif) 成立,只需
成立,只需.files/image298.gif) 成立,即
成立,即.files/image300.gif)
.files/image250.gif) 使
使.files/image181.gif) 成立的正整数n的最小值为5…………………………………12分
成立的正整数n的最小值为5…………………………………12分
18、解:(1)解法一:“有放回摸两次,颜色不同”指“先白再黑”或“先黑再白”,记“有放回摸球两次,两球恰好颜色不同”为事件A,
.files/image270.gif) “两球恰好颜色不同”共2×4+4×2=16种可能,
“两球恰好颜色不同”共2×4+4×2=16种可能,.files/image250.gif)
.files/image306.gif) ………………4分
………………4分
解法二:“有放回摸取”可看作独立重复实验 .files/image270.gif) 每次摸出一球得白球的概率为
每次摸出一球得白球的概率为.files/image308.gif)
.files/image250.gif) “有放回摸两次,颜色不同”的概率为
“有放回摸两次,颜色不同”的概率为.files/image310.gif) ………………………4分
………………………4分
(2)设摸得白球的个数为.files/image312.gif) ,依题意得
,依题意得
.files/image314.gif) ……
……
…………………………………………………………………………………………10分
.files/image316.gif) ……………………………………………………12分
……………………………………………………12分
19、证明:(1).files/image318.gif) 平面
平面.files/image189.gif)
.files/image250.gif) 平面
平面.files/image322.gif) 平面
平面.files/image189.gif) ,
,
又.files/image325.gif) 平面
平面.files/image207.gif)
.files/image250.gif) 侧面
侧面.files/image205.gif) 侧面
侧面.files/image207.gif) ……………………4分
……………………4分
(2).files/image270.gif)
.files/image197.gif) 为
为.files/image201.gif) 的中点,
的中点,.files/image333.gif)
.files/image335.gif)
.files/image336.jpg) 又
又.files/image270.gif) 侧面
侧面.files/image205.gif) 侧面
侧面.files/image207.gif) 从而
从而.files/image339.gif) 侧
侧.files/image210.gif) 故
故.files/image342.gif) 的长就是点
的长就是点.files/image191.gif) 到侧面
到侧面.files/image210.gif) 的距离在等腰
的距离在等腰.files/image345.gif) 中,
中,.files/image347.gif) ……………………………………8分
……………………………………8分
说明:亦可利用向量的方法求得
(3)几何方法:可以证明.files/image349.gif) 就是二面角
就是二面角.files/image212.gif) 的
的
平面角……………………………………10分
从而.files/image352.gif) ………………13分
………………13分
亦可利用等积转换算出.files/image199.gif) 到平面
到平面.files/image355.gif) 的高,
的高,
从而得出二面角.files/image212.gif) 的平面角为
的平面角为.files/image357.gif) ……13分
……13分
说明:也可以用向量法:平面.files/image359.gif) 的法向量为
的法向量为.files/image361.gif)
平面.files/image355.gif) 的法向量为
的法向量为.files/image364.gif) ………………10分
………………10分
.files/image366.gif)
.files/image250.gif) 二面角
二面角.files/image212.gif) 的平面角为
的平面角为.files/image369.gif)
20、解(1)设双曲线方程为.files/image371.gif)
由已知得.files/image373.gif) ,再由
,再由.files/image375.gif) ,得
,得.files/image377.gif)
故双曲线.files/image379.gif) 的方程为
的方程为.files/image381.gif) .…………………………………………5分
.…………………………………………5分
(2)将.files/image383.gif) 代入
代入.files/image381.gif) 得
得.files/image386.gif)
由直线.files/image093.gif) 与双曲线交与不同的两点得
与双曲线交与不同的两点得.files/image389.gif)
即.files/image391.gif) 且
且.files/image393.gif) . ① 设
. ① 设.files/image395.gif) ,则…………………8分
,则…………………8分
.files/image397.gif) ,由
,由.files/image220.gif) 得
得.files/image400.gif) ,
,
而.files/image402.gif)
.files/image404.gif) .…………………………11分
.…………………………11分
于是.files/image406.gif) ,即
,即.files/image408.gif) 解此不等式得
解此不等式得.files/image410.gif) ②
②
由①+②得.files/image412.gif)
故的取值范围为.files/image414.gif) …………………………………13分
…………………………………13分
21、解:(1)由题设知.files/image416.gif) ,又
,又.files/image418.gif) ,得
,得.files/image420.gif) ……………2分
……………2分
(2).files/image422.gif) …………………………………………………3分
…………………………………………………3分
由题设知.files/image234.gif) 时
时.files/image425.gif)
.files/image427.gif)
.files/image429.gif) …………………………………………………4分
…………………………………………………4分
.files/image250.gif)
.files/image432.gif) (当
(当.files/image032.gif) 时,取最小值)……………………4分
时,取最小值)……………………4分
而.files/image435.gif) 时,当且仅当
时,当且仅当.files/image032.gif) 时
时.files/image437.gif)
.files/image439.gif) …………………7分
…………………7分
(3).files/image236.gif) 时,方程
时,方程.files/image238.gif) 变形为
变形为.files/image443.gif)
令.files/image445.gif) 得
得.files/image447.gif) ………9分
………9分
由.files/image449.gif) ,得
,得.files/image451.gif) 或
或.files/image453.gif) ,
,
由.files/image455.gif) ,得
,得.files/image457.gif) ………………………………11分
………………………………11分
又因为.files/image459.gif)
.files/image461.jpg) 故
故.files/image463.gif) 在
在.files/image465.gif) 取得唯一的极小值
取得唯一的极小值.files/image467.gif)
又当.files/image469.gif) 时,
时,.files/image463.gif) 的值
的值.files/image472.gif) ,当
,当.files/image474.gif) 时,
时,
.files/image463.gif) 的值
的值.files/image477.gif) ,函数
,函数.files/image479.gif) 和
和.files/image481.gif) 草图如右
草图如右
两图像由公共点时,方程有解,.files/image483.gif) ,
,
故.files/image240.gif) 的最小值为
的最小值为.files/image467.gif) ,………………………………………………13分
,………………………………………………13分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com