纵坐标不变   
另解:    ……12分 以上每一个变换过程均为3分. 17.(本题满分12分) 解:(Ⅰ)在图1中,可得 ,从而 ,从而 ,故 ,故 取 中点 中点 连结 连结 ,则 ,则 ,又面 ,又面  面 面 , , 面  面 面  , , 面 面 ,从而 ,从而 平面 平面 ,
……4分 ,
……4分 ∴
又 , , , , ∴ 平面 平面 ……6分
……6分 另解:在图1中,可得 ,从而 ,从而 ,故 ,故 ∵面  面 面 ,面 ,面  面 面  , , 面 面 ,从而 ,从而 平面 平面 (Ⅱ)建立空间直角坐标系 如图所示,则 如图所示,则 , , , ,  , , ……8分
……8分
 设 设 为面 为面 的法向量, 的法向量,
则 即 即 ,解得 ,解得 令 ,可得 ,可得 又 为面 为面 的一个发向量 的一个发向量 ∴ ∴二面角 的余弦值为 的余弦值为 . . ……12分 18.(本题满分14分) 解:(Ⅰ)合格率分别为0.798,0.801,0.803,0.798,0.8 该产品的合格率最接近于数值0.8,即 =0.8
……6分 =0.8
……6分 (Ⅱ)设8500件产品中合格产品的数量为 , , 则 为随机变量且 为随机变量且 ……9分 ……9分 故 (件), ……11分 (件), ……11分 即预测2009年该产品的合格产品数量为6800件. 从而经营利润为 (万元) (万元) ……14分  19.(本题满分14分) 19.(本题满分14分)
解:在 中, 中, ,则 ,则  ……1分 ……1分
(Ⅰ)方法一、设 ( ( ), ), 点 到 到 的距离之和为 的距离之和为  …5分 …5分
 ,令 ,令 即 即 ,又 ,又 ,从而 ,从而
当 时, 时, ;当 ;当 时, 时,  . . ∴当 时, 时, 取得最小值 取得最小值 此时 ,即点 ,即点 为 为 的中点. ……8分 的中点. ……8分 方法二、设点 ,则 ,则 到 到 的距离之和为 的距离之和为  ,求导得 ,求导得 ……5分 ……5分
由 即 即 ,解得 ,解得 当 时, 时, ;当 ;当 时, 时,  ∴当 时, 时, 取得最小值,此时点 取得最小值,此时点 为 为 的中点.
……8分 的中点.
……8分 (Ⅱ)设点 ,则 ,则 , , 点 到 到 三点的最远距离为 三点的最远距离为 ①若 即 即 ,则 ,则 ; ; ②若 即 即 ,则 ,则 ; ; ∴ ……11分
……11分 当 时, 时, 在 在 上是减函数,∴ 上是减函数,∴ 当 时, 时, 在 在 上是增函数,∴ 上是增函数,∴ ∴当 时, 时,  ,这时点 ,这时点 在 在 上距 上距 点 点 .
……14分 .
……14分 20.(本题满分14分) (I)解: 三点共线,设 三点共线,设 ,则 ,则  ,………………………………………………2分 ,………………………………………………2分
化简得: ,所以 ,所以 所以 =1。……………………………………………………………………………4分 =1。……………………………………………………………………………4分 (II)由题设得 …… 6分 …… 6分 即 ( ( ),∴ ),∴ 是首项为 是首项为 ,公差为2的等差数列,通项公式为 ,公差为2的等差数列,通项公式为 …8分 …8分 (III)由题设得 ,……10分 ,……10分 令 ,则 ,则 .所以 .所以 是首项为 是首项为 ,公比为 ,公比为 的等比数列, 的等比数列, 通项公式为 .…………………………………………………12分 .…………………………………………………12分 由 解得 解得 ?????????????????????????????????????????????????????? 14分 ?????????????????????????????????????????????????????? 14分 21.(本题满分14分) 解:(Ⅰ)设点  ,依题意可得 ,依题意可得  …………………………2分 …………………………2分
整理得
故动点 的轨迹方程为 的轨迹方程为 .
…………………………4分 .
…………………………4分
(Ⅱ)将直线 的方程 的方程 代入圆 代入圆 方程 方程
整理得
根据根与系数的关系得 , , ……① ……①
将直线 的方程 的方程 代入圆 代入圆 方程, 方程,
同理可得 , , ……② ……②
由①、②可得 ,所以结论成立. …………………………8分 ,所以结论成立. …………………………8分
(Ⅲ)设点 ,点 ,点 ,由 ,由 、 、 、 、 三点共线 三点共线 得 ,解得 ,解得 …………………………10分
…………………………10分
由 、 、 、 、 三点共线 三点共线 同理可得
由 变形得 变形得 即 ,
…………………………12分 ,
…………………………12分 从而 ,所以 ,所以 ,即 ,即 . …………………………14分 . …………………………14分 
| |

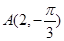 到直线
到直线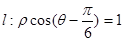 的距离为 .
的距离为 .
 到直线
到直线 的距离为 .
的距离为 . 10.
10. 11.
11. 12.
12. 13.
13.
 15.
15. 

 的最小正周期
的最小正周期 ,故
,故 ……3分
……3分 代入
代入 的解析式得
的解析式得 ,又
,又 ,
,
 的解析式为
的解析式为 ……6分
……6分
 (Ⅱ)变换过程如下:
(Ⅱ)变换过程如下: