
题目列表(包括答案和解析)
| 2 |
| x |
| p |
| x |
| 1 |
| 16 |
| ||
| 2 |
| 1 |
| e |
| 1 |
| e |
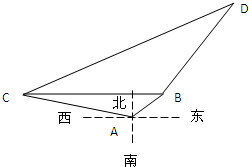 在海岸A处,发现北偏东45°方向,距离A为(
在海岸A处,发现北偏东45°方向,距离A为(| 3 |
| 3 |
| p |
| x |
| 1 |
| e |
| 1 |
| e |
| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
某学生社团在对本校学生学习方法开展问卷调查的过程中发现,在回收上来的1000份有效问卷中,同学们背英语单词的时间安排共有两种:白天背和晚上临睡前背。为研究背单词时间安排对记忆效果的影响,该社团以5%的比例对这1000名学生按时间安排类型进行分层抽样,并完成一项实验,实验方法是,使两组学生记忆40个无意义音节(如XIQ、GEH),均要求在刚能全部记清时就停止识记,并在8小时后进行记忆测验。不同的是,甲组同学识记结束后一直不睡觉,8小时后测验;乙组同学识记停止后立刻睡觉,8小时后叫醒测验。
两组同学识记停止8小时后的准确回忆(保持)情况如图(区间含左端点而不含右端点)
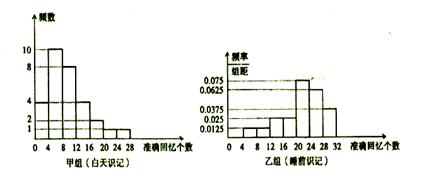
(1)估计1000名被调查的学生中识记停止后8小时40个音节的保持率大于等于60%的人数;
(2)从乙组准确回忆因结束在[12,24)范围内的学生中随机选3人,记能准确回忆20个以上(含20)的人数为随机变量X,求X分布列及数学期望;
(3)从本次实验的结果来看,上述两种时间安排方法中哪种方法背英语单词记忆效果更好? 计算并说明理由。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com