
题目列表(包括答案和解析)
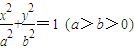 的离心率是
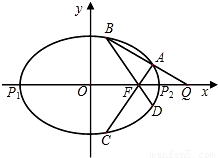
的离心率是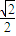 ,P1、P2是椭圆E的长轴的两个端点(P2位于P1右侧),点F是椭圆E的右焦点.点Q是x轴上位于P2右侧的一点,且满足
,P1、P2是椭圆E的长轴的两个端点(P2位于P1右侧),点F是椭圆E的右焦点.点Q是x轴上位于P2右侧的一点,且满足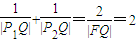 .
.
 (a>b>0)的两个焦点为F1(-c,0)、F2(c,0)和顶点B1、B2构成面积为32的正方形.
(a>b>0)的两个焦点为F1(-c,0)、F2(c,0)和顶点B1、B2构成面积为32的正方形. ).问:A、B两点能否关于直线PQ对称.若能,求出kk的取值范围;
).问:A、B两点能否关于直线PQ对称.若能,求出kk的取值范围;
 (a>b>0)的两个焦点为F1(-c,0)、F2(c,0)和顶点B1、B2构成面积为32的正方形.
(a>b>0)的两个焦点为F1(-c,0)、F2(c,0)和顶点B1、B2构成面积为32的正方形. ).问:A、B两点能否关于直线PQ对称.若能,求出kk的取值范围;
).问:A、B两点能否关于直线PQ对称.若能,求出kk的取值范围;
已知点A(0,2)和圆C:(x-6)2+(y-4)2=![]() ,一条光线从A点出发射到x轴上后沿圆的切线方向反射,求这条光线从A点到切点所经过的路程.
,一条光线从A点出发射到x轴上后沿圆的切线方向反射,求这条光线从A点到切点所经过的路程.
思路分析:先画出示意图,再利用对称性求解问题.类似这种关于光的反射问题,通常都利用对称性作出题中图形对“镜面”的对称图形,从而化折线问题为直线问题.
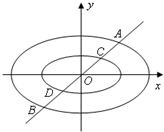 定义:由椭圆的两个焦点和短轴的一个顶点组成的三角形称为该椭圆的“特征三角形”.如果两个椭圆的“特征三角形”是相似的,则称这两个椭圆是“相似椭圆”,并将三角形的相似比称为椭圆的相似比.已知椭圆C1:
定义:由椭圆的两个焦点和短轴的一个顶点组成的三角形称为该椭圆的“特征三角形”.如果两个椭圆的“特征三角形”是相似的,则称这两个椭圆是“相似椭圆”,并将三角形的相似比称为椭圆的相似比.已知椭圆C1:| x2 |
| 4 |
| x2 |
| 16 |
| y2 |
| 4 |
| x2 |
| a2 |
| y2 |
| b2 |
| x2 |
| a2 |
| y2 |
| b2 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com