
题目列表(包括答案和解析)
 15、如图,D、E分别在△ABC的AB、AC边上,且DE与BC不平行,要使△ABC与△AED相似,需要添加一个条件
15、如图,D、E分别在△ABC的AB、AC边上,且DE与BC不平行,要使△ABC与△AED相似,需要添加一个条件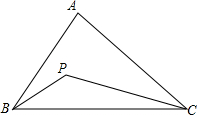 点P是△ABC内一点,要想知道△BPC与△ABC的面积之比,只有一把仅有刻度的直尺,须要度量的最少的次数是
点P是△ABC内一点,要想知道△BPC与△ABC的面积之比,只有一把仅有刻度的直尺,须要度量的最少的次数是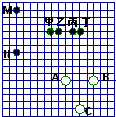 如图,棋盘上有三个白棋子A,B,C和两个黑棋子M,N,要使△ABC与△MNP相似,那么第三个黑棋子P应该放在甲乙丙丁哪个点上.答:应该在
如图,棋盘上有三个白棋子A,B,C和两个黑棋子M,N,要使△ABC与△MNP相似,那么第三个黑棋子P应该放在甲乙丙丁哪个点上.答:应该在湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com