
题目列表(包括答案和解析)
| 1 |
| 6 |
. |
| BC |
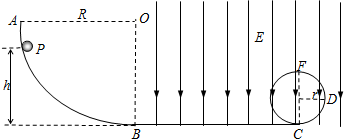
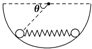 如图所示,在一内壁光滑的半圆球壳内有两个可视为质点的小球用一劲度系数为k的轻弹簧连接着,已知球壳固定且内半径为R,两小球质量均为m.两小球与弹簧静止时处在同一水平线上,小球与球壳球心连线与水平方向成θ角,弹簧形变在弹性限度范围内,则弹簧的原长为( )
如图所示,在一内壁光滑的半圆球壳内有两个可视为质点的小球用一劲度系数为k的轻弹簧连接着,已知球壳固定且内半径为R,两小球质量均为m.两小球与弹簧静止时处在同一水平线上,小球与球壳球心连线与水平方向成θ角,弹簧形变在弹性限度范围内,则弹簧的原长为( )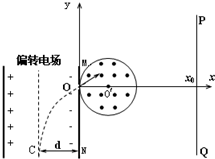 如图所示,在平面坐标系xOy内,同种带正电离子,质量m=1.0×10-20kg、带电量q=1.0×10-10C,以相同速度不断从C点垂直射入匀强电场,偏转后通过极板MN上的小孔O离开电场时的速度大小为v=2.0×106m/s,方向与x轴成30°角斜向上.在y轴右侧有一个圆心位于O'(0.01m,0)点,半径r=0.01m的圆形磁场区域,磁场方向垂直纸面向外,磁感应强度B=0.01T,有一垂直于x轴的面积足够大的竖直荧光屏PQ置于坐标x0=0.04m处.已知NC之间的距离d=0.02m.试求:
如图所示,在平面坐标系xOy内,同种带正电离子,质量m=1.0×10-20kg、带电量q=1.0×10-10C,以相同速度不断从C点垂直射入匀强电场,偏转后通过极板MN上的小孔O离开电场时的速度大小为v=2.0×106m/s,方向与x轴成30°角斜向上.在y轴右侧有一个圆心位于O'(0.01m,0)点,半径r=0.01m的圆形磁场区域,磁场方向垂直纸面向外,磁感应强度B=0.01T,有一垂直于x轴的面积足够大的竖直荧光屏PQ置于坐标x0=0.04m处.已知NC之间的距离d=0.02m.试求: 如图所示,在平面直角坐标系xOy平面内,有以(r,0)为圆心、半径为r的圆形匀强磁场区域,磁场的磁感应强度大小为B,方向垂直于xOy平面向里.在y=r的上方足够大的范围内,有沿x轴负方向的匀强电场,电场强度的大小为E.从O点向偏右的不同方向发射速度大小相同的质子,质子的运动轨迹均在xOy平面内.已知质子在磁场中运动的轨道半径也为r,质子的电荷量为e,质量为m,不计质子的重力及所受的阻力.
如图所示,在平面直角坐标系xOy平面内,有以(r,0)为圆心、半径为r的圆形匀强磁场区域,磁场的磁感应强度大小为B,方向垂直于xOy平面向里.在y=r的上方足够大的范围内,有沿x轴负方向的匀强电场,电场强度的大小为E.从O点向偏右的不同方向发射速度大小相同的质子,质子的运动轨迹均在xOy平面内.已知质子在磁场中运动的轨道半径也为r,质子的电荷量为e,质量为m,不计质子的重力及所受的阻力.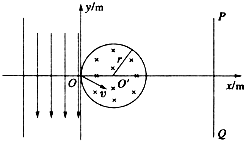 如图所示,在xOy平面内,y轴左侧有一个方向竖直向下,水平宽度为l=
如图所示,在xOy平面内,y轴左侧有一个方向竖直向下,水平宽度为l=| 3 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com