
题目列表(包括答案和解析)
| 1 | 2 |

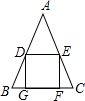 如图,△ABC中,AB=AC,AB、AC中点D、E,点G、F在BC上,DEFG为正方形,DE=2cm,则AC的长为( )
如图,△ABC中,AB=AC,AB、AC中点D、E,点G、F在BC上,DEFG为正方形,DE=2cm,则AC的长为( )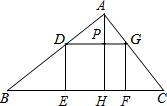 .已知BC=12,AH=8.
.已知BC=12,AH=8. (2013•威海)如图,在△ABC中,∠ACB=90°,BC的垂直平分线EF交BC于点D,交AB于点E,且BE=BF,添加一个条件,仍不能证明四边形BECF为正方形的是( )
(2013•威海)如图,在△ABC中,∠ACB=90°,BC的垂直平分线EF交BC于点D,交AB于点E,且BE=BF,添加一个条件,仍不能证明四边形BECF为正方形的是( )阅读材料,解答问题。(12分)
 已知:锐角
已知:锐角![]() ,如图,求作:正方形DEFG,使D、E落在BC边上,F、G分别落在AC、AB边上。
,如图,求作:正方形DEFG,使D、E落在BC边上,F、G分别落在AC、AB边上。
作法:(1)画一个有三个顶点落在![]() 两边上的正方形D1、E1、F1、G1
两边上的正方形D1、E1、F1、G1
(如图所示);
(2)连结BF,并延长交AC于点F;
(3)过点F作EF⊥BC于点E;
(4)过F作FG//BC,交AB于点G;
(5)过点G作GD⊥BC于点D;则四边形DEFG即为所求作的正方形。
问题:(1)说明上述所求作四边形DEFG为正方形的理由。
![]() (2)在
(2)在![]() 中,如果BC=120,BC边上的高为80,求上述正方形DEFG的边长。
中,如果BC=120,BC边上的高为80,求上述正方形DEFG的边长。
(3)若把(2)中的正方形DEFG改为矩形DEFG,且GF= DG,其他条件不变,此时,GF是多少?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com