为了解某小型企业职工喜爱运动是否与性别有关，对本企业50人进行了问卷调查得到了如下的列联表：

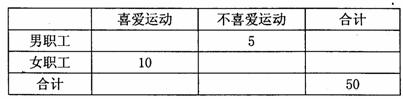
       已知在全部50人中随机抽取1人抽到喜爱运动的职工的概率为．

    （1）请将上面的列联表补充完整（不用写计算过程）；

    （2）能否在犯错误的概率不超过0．005的前提下认为喜爱运动与性别有关？

       说明你的理由：

    （3）现从女职工中抽取2人进一步调查，设其中喜爱运动的女职工人数为，求的分布列与期望，

    下面的临界值表供参考：

       （参考公式：，其中

（本小题满分12分）

已知函数f（x）是定义在[-e,0）∪（0,e]上的奇函数，当x∈（0,e],f（x）=ax+lnx（其中e是自然对数的底数，a∈R）

   （1）求f（x）的解析式；

   （2）设g（x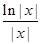）=,x∈[-e,0）,求证：当a=-1时，f（x）>g（x）+;

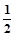   （3）是否存在实数a，使得当x∈[-e,0）时f（x）的最小值是3 如果存在，求出实数a的值；如果不存在，请说明理由．