
题目列表(包括答案和解析)
(1)分别对男、女学生抽取一个容量相同的样本,样本容量可在40—50之间选择.若高一男、女学生各抽取的人数定为18人,那么高二、高三男、女学生的人数各应定为多少?
(2)上述描样采用的是哪种抽样方法?所得男、女学生的样本容量是多少?
(3)如果按照上述抽样方法采集的各样本数据如下表(单位:分)
样本数据 (单位∶分) | 男生 | 女生 | |
一年级 | 380 500 245 450 145 620 480 420 520 280 550 660 350 500 330 600 180 520 | 230 460 600 110 420 105 580 400 420 380 180 500 140 450 600 400 125 540 | |
二年级 | 420 580 510 175 280 630 400 150 450 360 450 330 400 420 300 500 580 400 | 280 380 530 95 190 570 300 220 320 250 300 350 400 360 130 450 590 230 | |
三年级 | 380 420 235 125 400 470 330 200 420 280 300 410 | 200 460 165 400 75 430 300 220 250 130 270 340 | |
求相应于男生标本的平均数![]() 男,标准差s男,相应于女生样本的平均均数
男,标准差s男,相应于女生样本的平均均数![]() 女,标准差s女,和男、女学生全体组成的新样本的平均数x、标准差s.根据以上结果作出估计分析.
女,标准差s女,和男、女学生全体组成的新样本的平均数x、标准差s.根据以上结果作出估计分析.
| A、角度和它的正切值 | B、人的右手一柞长和身高 | C、正方体的棱长和表面积 | D、真空中自由落体运动物体的下落距离和下落时间 |
为了考察两个变量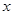 和
和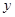 之间的线性相关性,甲、乙两位同学各自独立地做100次和150次试验,并且利用线性回归方法,求得回归直线分别为
之间的线性相关性,甲、乙两位同学各自独立地做100次和150次试验,并且利用线性回归方法,求得回归直线分别为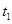 和
和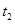 ,已知两人在试验中发现对变量
,已知两人在试验中发现对变量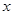 的观测数据的平均值都是
的观测数据的平均值都是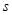 ,对变量
,对变量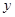 的观测数据的平均值都是
的观测数据的平均值都是 ,那么下列说法正确的是( )
,那么下列说法正确的是( )
 .
.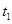 和
和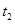 有交点
有交点
 .
.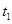 与
与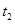 相交,但交点不一定是
相交,但交点不一定是
 .
.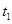 与
与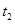 必定平行
必定平行
 .
. 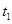 与
与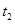 必定重合
必定重合
在一次积分游戏活动中,两
同学约定游戏规则为:盒中装有10张写有积分的卡片,其中有1张为50分,有3张为10分,其余6张为0分;每人从盒中任抽2张卡片,计算两张卡片上的积分和,并按积分和的大小确定两人的胜负,若积分和相等,则本局为平局.现同学甲从盒中任抽2张卡片,求:(1)同学甲
积分和不为0的概率;(2)同学甲
积分和ξ的概率分布列和期望Eξ.如图,AB、CD是两个等圆的直径,AB∥CD,AD、BC与两圆相切,作两圆的公切线EF,切点分别为F1、F2,交BA、DC的延长线于E、F,交AD于G1,交BC于G2.设EF与BC、CD的交角分别为![]() 、
、![]() .
.
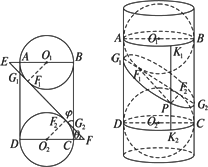
(1)G2F1+G2F2________AD,
(2)G1G2________AD,
(3)![]() ________cos
________cos![]() ________sin
________sin![]() .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com