题目列表(包括答案和解析)
甲、乙两人独立地破译1个密码, 他们能译出密码的概率分别为
和
, 求:
(1)甲、乙两人至少有一个人破译出密码的概率;
(2)两人都没有破译出密码的概率.
甲、乙两人独立地破译1个密码，他们能译出密码的概率分别为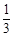
和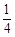
，求（1）恰有1人译出密码的概率；
（2）若达到译出密码的概率为
，至少需要多少个乙这样的人？
【解析】第一问中，考虑两种情况，是甲乙中的那个人译出密码，然后利用互斥事件概率公式相加得到。
第二问中，利用间接法n个乙这样的人都译不出密码的概率为
．可以得到结论。
解：设“甲译出密码”为事件A；“乙译出密码”为事件B，则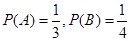
．
（1）
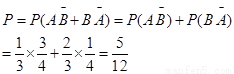………………5分
（2）n个乙这样的人都译不出密码的概率为．
．解得．
达到译出密码的概率为99/100，至少需要17人.
样本容量为n，组数为P，第i组的频数为k，则该组频率为________，若前i－1组的累积频率(前n－1组的频率之和)为m，则前i组的累积频率为________．
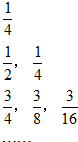（2006•朝阳区一模）如表给出一个“直角三角形数阵”满足每一列成等差数列，从第三行起每一行的数成等比数列，且每一行的公比相等，记第i行，第j列的数为aij（i≥j，i，j∈N*），则第1列的公差等于| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
（2008•临沂二模）如图，给出了一个三角形数阵，已知每一列的数成等差数列，从第3行起，每一行的数成等比数列，每一行的公比都相等．记第i行第j列的数为aij（i≥j，i，j∈N*）湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com