
题目列表(包括答案和解析)
阅读后回答下列问题.
线段垂直平分线定理:线段垂直平分线上的点到线段两端点的距离相等,将其写成“如果……那么……”的形式,则为:如果一个点在线段的垂直平分线上,那么这个点在线段两端点的距离相等,将这个命题的题设与结论交换位置,则有:如果一个点到线段两端点的距离相等,那么这个点在线段的垂直平分线上.这是一个真命题,以又称为线段垂直平分线的逆定理.
请把下列定理改成“如果……那么……”的形式,写出它们的逆命题,并判断其逆命题是真命题还是假命题.
(1)角平分线上的点到角的两边距离相等;
(2)两直线平行,同位角相等.
(3)对顶角相等.
如图,已知∠AOB和一条定长线段a,在∠AOB内找一点P,使P到角的两边OA、OB的距离都等于a.
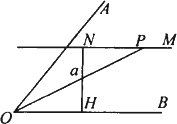
作法:①在∠AOB内作OB的垂线段NH,使NH=a,H为垂足;②过N作NM∥OB;③作∠AOB的平分线OP,与MN交于点P;④点P即为所求,其中③的依据是
A.平行线间的距离处处相等
B.到角的两边等距离的点在角的平分线上
C.角的平分线上的点到角的两边等距离
D.到线段两端等距离的点在这条线段的垂直平分线上
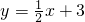 与x轴、y轴分别交于A、B两点,直线y=kx+8与直线AB相交于点D,与x轴相交于点C,过D作DE⊥x轴,E为垂足,E点的横坐标为2.
与x轴、y轴分别交于A、B两点,直线y=kx+8与直线AB相交于点D,与x轴相交于点C,过D作DE⊥x轴,E为垂足,E点的横坐标为2.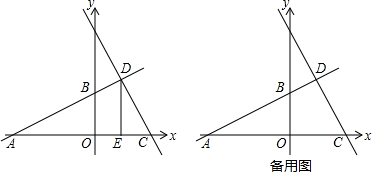
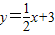 与x轴、y轴分别交于A、B两点,直线y=kx+8与直线AB相交于点D,与x轴相交于点C,过D作DE⊥x轴,E为垂足,E点的横坐标为2.
与x轴、y轴分别交于A、B两点,直线y=kx+8与直线AB相交于点D,与x轴相交于点C,过D作DE⊥x轴,E为垂足,E点的横坐标为2.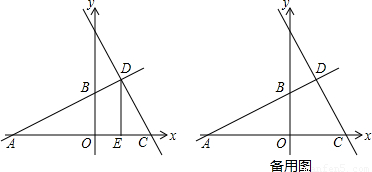
 ,则它们组成一个等腰直角三角形;
,则它们组成一个等腰直角三角形;湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com