
题目列表(包括答案和解析)
| a |
| b |
| a |
| b |
| c |
| c |
| a |
| b |
 ,
, },其中
},其中 ,
, 是不共线向量,B={
是不共线向量,B={ |
|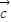 与
与 ,
,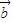 共面的任意向量},则A和B不可能具有相同的势;
共面的任意向量},则A和B不可能具有相同的势;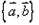 ,其中
,其中  是不共线向量,B={
是不共线向量,B={ 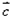 |
|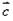 与
与 共面的任意向量},则A和B不可能具有相同的势;
共面的任意向量},则A和B不可能具有相同的势; 定义:对于映射f:A→B,如果A中的不同元素有不同的象,且B中的每一个元素都有原象,则称f:A→B为一一映射.如果存在对应关系φ,使A到B成为一一映射,则称A和B具有相同的势.给出下列命题:
①A={奇数},B={偶数},则A和B具有相同的势;
②A是直角坐标系平面内所有点形成的集合,B是复数集,则A和B不具有相同的势;
③若A={![]() ,
,![]() },其中
},其中![]() ,
,![]() 是不共线向量,B={
是不共线向量,B={![]() |
|![]() 与
与![]() ,
,![]() 共面的任意向量},则A和B不可能具有相同的势;
共面的任意向量},则A和B不可能具有相同的势;
④若区间A=(-1,1),B=(-∞,+∞),则A和B具有相同的势.
其中真命题为________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com