练习册

  • 练习册
  • 试题
    (一)知识教学点 掌握利用平面的基本性质证明诸点共面.诸线共面.三点共线.三线共点问题的一般方法． 1．证明若干点或直线共面通常有两种思路 (1)先由部分元素确定若干平面.再证明这些平面重合.如例1之①, (2)先由部分元素确定一个平面.再证明其余元素在这平面内.如例1之②． 2．证明三点共线.通常先确定经过两点的直线是某两个平面的交线.再证明第三点是这两个平面的公共点.即该点分别在这两个平面内.如例2． 3．证明三线共点通常先证其中的两条直线相交于一点.然后再证第三条直线经过这一点.如练习． 【查看更多】

     

    题目列表(包括答案和解析)

    利用不等式的基本性质用“﹥”或“﹤”填空．

    (1)如果a﹥b，c﹥d，那么a＋c ________ b＋d；

    (2)如果a﹥b﹥0，c﹥d﹥0，那么ac ________ bd _________ 0；

    (3)a﹥b﹥0，那么______；

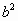    (4)a﹥b﹥0，那么．

    完成答题后，与同学交流体会，并总结一般的规律．

    查看答案和解析>>

    下列命题中，正确命题的个数为(　　)

    ①平面的基本性质1可用集合符号叙述为：若A∈l，B∈l，且A∈α，B∈α，则必有l∈α；

    ②四边形的两条对角线必相交于一点；

    ③用平行四边形表示的平面，以平行四边形的四条边作为平面的边界线；

    ④平行四边形是平面图形．

    A．1个                  B．2个         C．3个                  D．4个

    查看答案和解析>>

    （2012•卢湾区一模）已知函数f（x）=
    x+1-tt-x
    （t为常数）．
    （1）当t=1时，在图中的直角坐标系内作出函数y=f（x）的大致图象，并指出该函数所具备的基本性质中的两个（只需写两个）．
    （2）设an=f（n）（n∈N*），当t＞10，且t∉N*时，试判断数列{an}的单调性并由此写出该数列中最大项和最小项（可用[t]来表示不超过t的最大整数）．
    （3）利用函数y=f（x）构造一个数列{xn}，方法如下：对于给定的定义域中的x1，令x2=f（x1），x3=f（x2），…，xn=f（xn-1）（n≥2，n∈N*），…在上述构造过程中，若xi（i∈N*）在定义域中，则构造数列的过程继续下去；若xi不在定义域中，则构造数列的过程停止．若可用上述方法构造出一个常数列{xn}，求t的取值范围．

    查看答案和解析>>

    （2012•卢湾区一模）已知函数f（x）=
    x+1-tt-x
    （t为常数）．
    （1）当t=1时，在图中的直角坐标系内作出函数y=f（x）的大致图象，并指出该函数所具备的基本性质中的两个（只需写两个）．
    （2）设an=f（n）（n∈N*），当t＞10，且t∉N*时，试判断数列{an}的单调性并由此写出该数列中最大项和最小项（可用[t]来表示不超过t的最大整数）．
    （3）利用函数y=f（x）构造一个数列{xn}，方法如下：对于给定的定义域中的x1，令x2=f（x1），x3=f（x2），…，xn=f（xn-1）（n≥2，n∈N*），…在上述构造过程中，若xi（i∈N*）在定义域中，则构造数列的过程继续下去；若xi不在定义域中，则构造数列的过程停止．若取定义域中的任一值作为x1，都可以用上述方法构造出一个无穷数列{xn}，求实数t的值．

    查看答案和解析>>

    （2009•闸北区二模）和平面解析几何的观点相同，在空间中，空间曲面可以看作是适合某种条件的动点的轨迹．一般来说，在空间直角坐标系O-xyz中，空间曲面的方程是一个三元方程F（x，y，z）=0．
    （Ⅰ）在直角坐标系O-xyz中，求到定点M0（0，2，-1）的距离为3的动点P的轨迹（球面）方程；
    （Ⅱ）如图，设空间有一定点F到一定平面α的距离为常数p＞0，即|FM|=2，定义曲面C为到定点F与到定平面α的距离相等（|PF|=|PN|）的动点P的轨迹，试建立适当的空间直角坐标系O-xyz，求曲面C的方程；  
    （Ⅲ）请类比平面解析几何中对二次曲线的研究，讨论曲面C的几何性质．并在图中通过画出曲面C与各坐标平面的交线（如果存在）或与坐标平面平行的平面的交线（如果必要）表示曲面C的大致图形．画交线时，请用虚线表示被曲面C自身遮挡部分．

    查看答案和解析>>


    同步练习册答案