题目列表(包括答案和解析)
(1). 如图所示为一种测量电源电动势的电路原理图. E为供电电源，ES为标准电源，EX为待测电源，RP是限流电阻，R0是电流表的保护电阻，AB是均匀电阻丝，长度为L. 闭合S1进行测量时，先将S2合到“1”位置，移动C至C1处时，恰好使电流表指针指零，测得AC1=
；再将S2合到“2”位置，移动C至C2处时，恰好又使电流表指针指零，测得AC2= 
L. 请你根据这些信息，结合所学过的有关物理知识回答：
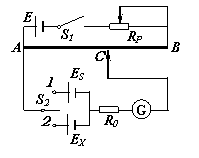
①本实验对供电电源的要求是E ES和EX
( 填“＜”,“＝”或“＞”) ；
②你认为该实验中电流表最好应选用_______
(填“安培表”，“毫安表”，“微安表”，“灵敏电流计”) ;
③本次实验测得的EX = ES.
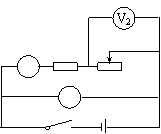
(2)．利用如图所示的电路测定电源的电动势和内电阻，提供的器材为（ ）
（A）干电池两节，每节电池的电动势约为1.5V，内阻未知
（B）直流电压表V1、V2，内阻很大 （C）直流电流表A，内阻可忽略不计
（D）定值电阻R0，阻值未知，但不小于5W （E）滑动变阻器 （F）导线和开关
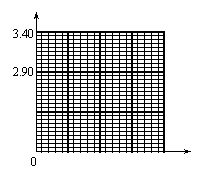
某同学利用该电路完成实验时，由于某根导线发生断路故障，因此只记录了一个电压表和电流表的示数，并描在了坐标纸上作出U--I图，如图所示。由图像可知，该同学测得两节干电池总的电动势值为__________V，总内阻为__________W。由计算得到的数据可以判断能够正确示数的电压表应为表__________（选填“V1”或“V2”）（保留三位有效数字）
利用如图所示的电路测定电源电动势和内电阻，提供的器材有：
A．干电池两节（每节电动势约1.5V，内阻未知） B．直流电压表V1、V2（内阻很大）
C． 直流电流表A（内阻可以忽略不计） D．定值电阻R（阻值未知，但不小于5Ω）
E．滑动变阻器 F．导线和开关
（1）甲同学利用该电路完成实验时，由于某根导线发生断路故障，因此只记录到了一个电压表和电流表的示数，如下表所示：
| U/V | 2．62 | 2．48 | 2．34 | 2．20 | 2．06 | 1．92 |
| I/A | 0．08 | 0．12 | 0．19 | 0．20 | 0．24 | 0．28 |
试利用表格中的数据在所给的坐标图中作出U—I图，由图像可知，该同学测得两节干电池总的电动势为 V，总内阻为 Ω。由计算得到的数据可以判断能够正确读数的电压表应该为表 （填“V1”或“V2”）
（2）乙同学在找出断路的导线并调换好的导线后，连接该电路继续实验时，由于电流表发生短路故障，因此只能记录下两个电压表示数，该同学利用记录的数据，以表V2示数U2为横坐标，表V1示数U1为纵坐标作图像，也得到一条不过原点的直线，已知直线的斜率为k，纵轴截距为b，则两节干电池总的电动势大小为 ，两节干电池总的内阻 （填“可以”或“不可以”）求出。
如果该同学希望通过利用图像的截距直接得到电源的电动势，保持U1为纵坐标不变，应该选用 作为横坐标作图。
 | |||
 | |||
题号
1
2
3
4
5
6
7
8
9
10
答案
C
B
D
D
B
D
A
B
D
D
11
12
13
14
15
16
17
18
19
20
21
D
B
C
B
B
AC
D
C
A
AC
CD
22 Ⅰ. 2.50（2分） 0.25（2分） 3.50 （3分）
Ⅱ ① 40K(或40×103) （3分）
② A，D，G，H (各1分，共4分)
③ 如图所示
23. (16分)
解：（1）m在滑动摩擦力的作用下向右加速时加速度达到最大am。
对m由牛顿第二定律得： f=mam ①. ………………..(1分)
f=μN ②.………………..(1分)
N=mg ③……………………(1分)
对M由牛顿第二定律得：F-f=MaM ④…………………(1分)
要使木板能抽出来则要求M的加速度aM大于am。即： aM>am …………...(1分)
解以上方程得： F>4N ……………………(1分)
（2）设F作用时间t1后，m在M上继续相对滑行t2后到M的最左端。
m所经过的位移Sm为：Sm= am(t1+t2)2/2 ⑤………………..(1分)
速度vm为：vm= am(t1+t2) ⑥..………………(1分)
F撤消后，M的加速度 aM2为 f=MaM2 ⑦..………………(1分)
M所经过的位移SM为：SM= aMt12/2 +aMt1t2- aM2t22/2 ⑧………………..(2分)
速度vM为：vM= aMt1- aM2t2 ⑨………………..(1分)
位移关系为： SM- Sm=L ……………….. ..(1分)
此时要求： vM≥ vm ……………….. ..(1分)
解①----⑨方程组及速度位移关系得： t1≥0.8s
……………….. ..(2分)
即力F的作用时间不得少于0.8 s
24 (18分)
解：（1）经加速电场加速：qU0=mv02/2 得v0=8×106m/s …………….. ..(2分)
垂直极板方向做匀加速直线运动，设加速度a，经1×10-8s的时间，侧向位移y
a=qu/md y=at2/2 得y=8×10-3m …………….. ..(3分)
电子进入极板后在平行极板方向做匀速直线运动，垂直极板方向沿同一方向先匀加速再匀减速，再匀加速．匀减速……
经过各n次匀加速．匀减速，则有 2y．n≤d/2
解得 n≤3.125 取n=3 …………….. ..(3分)
则经过加速．减速各3次后距板的距离为△y =d/2-2y×3=2×10-3m
对应的电势差△u=△yU/d=1.82V …………….. ..(2分)
∴电子离开电场时的动能 Ek=q(U0+△u)=183.8eV …………….. ..(3分)
（2）∵△y=y/4
电子在极板中运动的总时间为
……………..
..(3分)
∴极板长 L= v0t1=0.52m …………….. ..(2分)
25 （20分）
解：(1)从开始到M第一次着地，设着地速度为v1的过程中，对系统：
由机械能守恒定律：MgH-mgH=(M+m)v12/2 ①……..（2分）
由动量定理得： Mgt-mgt=(m+M)v1 ②……..（2分）
解得： t=1s …………(1分)
(2)设第3次着地时的速度为v3，此时系统损失的机械能△E1即为M的动能
△E1=Mv32/2 ③……….(1分)
m上升后落回速度仍为v3，绳绷直后达到共同速度v3′，损失能量△E2
绳绷直瞬间系统动量守恒，m的速度在M侧等效向上，与M同向：
m v3=(m+M) v3′ ④……….(2分)
△E2=mv32/2-(m+M) v3′2/2 ⑤………..(2分)
∴ △E1：△E2=4：1 ………….(1分)
(3)设M第一次着地后被m带着上升的高度为H1，
m v1=(m+M) v1′ ⑥……….(1分)
MgH1-mgH1=(M+m)v1′2/2 ⑦……….(2分)
解方程①⑥⑦可得 
……….(2分)
依此类推可得
……….(2分)
M所走的全部路程为 l=H+2H1+2H1+…2Hn=2.83m ……….(2分)
6
7
8
9
10
11
12
13
D
A
B
D
D
D
B
C
26．（1）4mol/L 溶液的密度 (4分)
（2）b (2分)
（3）2NaOH+2ClO2+H2O2====2NaClO2+2H2O+O2；防止H2O2分解 (3分)
（4）连续测定吸收塔内溶液的PH (2分)
（5）
(2分)
（6）b．e．d，重结晶 (4分)
27．（1）HCl；H2S；CH4 (每空1分，共3分)
（2）CH4(g)+2O2(g) ====CO2(g)+2H2O(l)；△H=-890KJ.mol-1 (3分)
（3）2PH3+4O2====P2O5+3H2O (3分)
|
====
(2分)
====
(2分)
(3分)
====
(2分)
?L-1
(3分)
的物质的量为
，若分解得到的固体产物全部为
，则m（残渣）=
，若
分解生成的残渣为
，则m（残渣）=
，
③调节和控制饮食，口服降血糖药物，提高受体对胰岛素的敏感度（4分，其他合理答案也可）