
题目列表(包括答案和解析)

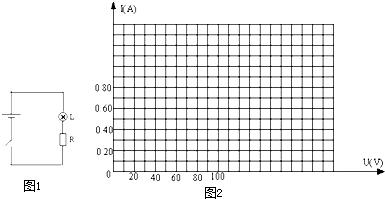
| 电流(A) | 0.20 | 0.37 | 0.50 | 0.60 | 0.68 | 0.75 | 0.78 | 0.79 | 0.80 | 0.80 |
| 电压(V) | 10.0 | 20.0 | 30.0 | 40.0 | 50.0 | 60.0 | 70.0 | 80.0 | 90.0 | 100.0 |
| 2 |
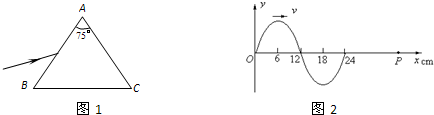
 是电流表,实验发现,当用某种频率的单色光照射K时,K会发出电子(光电效应),这时,即使A、K之间的电压等于零,回路中也有电流.当A的电势低于K时,当A比K的电势低到某一值Uc时,电流消失,Uc称为截止电压,当改变照射光的频率ν,截止电压Uc也将随之改变,其关系如图2所示,如果某次实验我们测出了画出这条图线所需的一系列数据,又知道了电子电量,则 ( )
是电流表,实验发现,当用某种频率的单色光照射K时,K会发出电子(光电效应),这时,即使A、K之间的电压等于零,回路中也有电流.当A的电势低于K时,当A比K的电势低到某一值Uc时,电流消失,Uc称为截止电压,当改变照射光的频率ν,截止电压Uc也将随之改变,其关系如图2所示,如果某次实验我们测出了画出这条图线所需的一系列数据,又知道了电子电量,则 ( )
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com