解：（1）OA=1，OC=2

则A点坐标为（0，1），C点坐标为（2，0）

设直线AC的解析式为y=kx+b

解得

直线AC的解析式为··················· 2分

（2）或

（正确一个得2分）························· 8分

（3）如图，设

过点作于F

由折叠知

或2··········· 10分

解：（1）由题意知，当、运动到秒时，如图①，过作交于点，则四边形是平行四边形．

∵，．

∴．

∴．

∴ ．解得．  5分

（2）分三种情况讨论：

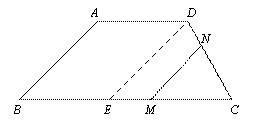
① 当时，如图②作交于，则有即．

∵，

∴，

∴，

解得． 6分

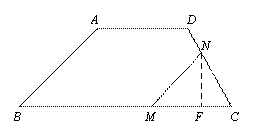
② 当时，如图③，过作于H．

则，

∴．

∴．7分

③ 当时，如图④．

则．

．      -------------------------------------8分

综上所述，当、或时，为等腰三角形．

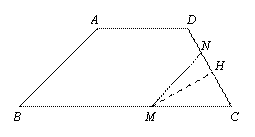
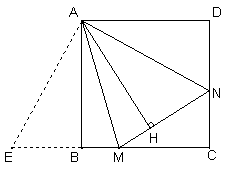
解：（1）如图①AH=AB

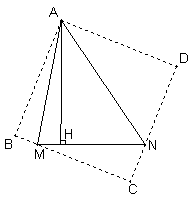
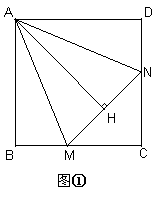（2）数量关系成立.如图②，延长CB至E，使BE=DN

∵ABCD是正方形

∴AB=AD，∠D=∠ABE=90°

∴Rt△AEB≌Rt△AND

∴AE=AN，∠EAB=∠NAD

∴∠EAM=∠NAM=45°

∵AM=AM

∴△AEM≌△ANM

∵AB、AH是△AEM和△ANM对应边上的高，

∴AB=AH

（3）如图③分别沿AM、AN翻折△AMH和△ANH，

得到△ABM和△AND

∴BM=2，DN=3，∠B=∠D=∠BAD=90°

分别延长BM和DN交于点C，得正方形ABCE．

由（2）可知，AH=AB=BC=CD=AD.                          

  设AH=x，则MC=,  NC=                             图②

在Rt⊿MCN中，由勾股定理，得

                                    

∴

解得.（不符合题意，舍去）

∴AH=6.

解：设这个正多边形的边数为n

由题意得：

解：根据题意，在平面直角坐标系中描出各点，可知四边形ABCD是矩形．由图形知，矩形的中心点E（5，3）．

由题意知，直线y=mx－3m＋2必过中心点E，所以有

3=m×5－3m＋2，解得m=．