
题目列表(包括答案和解析)
在二项式![]() 的展开式中,若所有项的系数之和等于64,那么n = .
的展开式中,若所有项的系数之和等于64,那么n = .
|
在二项式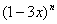 的展开式中,若所有项的系数之和等于64,那么在这个展开式中,
的展开式中,若所有项的系数之和等于64,那么在这个展开式中,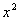 项的系数是
.(用数字作答)
项的系数是
.(用数字作答)
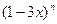 的展开式中,若所有项的系数之和等于64,那么在这个展开式中,
的展开式中,若所有项的系数之和等于64,那么在这个展开式中,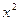 项的系数是 .(用数字作答)
项的系数是 .(用数字作答)已知二项式 的展开式中前三项的二项式系数之和为37.
的展开式中前三项的二项式系数之和为37.
(1)展开式中的第几项的系数最大,最大值是多少?
(2)是否存在关于x的整数次幂的项?若存在,求所有这样的项;若不存在,说明理由.
在二项式(1-3x)n的展开式中,若所有项的系数之和等于64,那么n=________,这个展开式中含x2项的系数是________.
一、选择题:本大题共12小题,每小题5分,满分60分。
1.C 2.D 3.A 4.B 5.A 6.D 7.B 8.C 9.A
10.B 11.D 12.C
二、填空题:本大题共4小题,每小题5分,满分20分。
13.64 14.卷.files/image130.gif) 15.4 16.
15.4 16.卷.files/image132.gif)
三、解答题:本大题共6小题,满分70分。
17.(本小题满分10分)
(1)解:∵卷.files/image134.gif) 2分
2分
∴卷.files/image136.gif)
∴卷.files/image138.gif)
∴卷.files/image140.gif) 5分
5分
(2)解:∵卷.files/image142.gif)
∴卷.files/image144.gif)
又∵卷.files/image146.gif) 7分
7分
∵卷.files/image148.gif) ,
,
∵卷.files/image150.gif)
=卷.files/image152.gif) 10分
10分
18.(本小题满分12分)
解:用Ai表示事件:一天之内第i个部件需要调整(i=1、2、3),
则卷.files/image154.gif) ,
,
用卷.files/image156.gif) 表示一天之内需要调整的部件数,则
表示一天之内需要调整的部件数,则
(1)卷.files/image158.gif) ……3分
……3分
(2)卷.files/image160.gif)
卷.files/image162.gif) ……………………12分
……………………12分
答:一天之内恰有一个部件需要调整的概率是0.398;一天之内至少有两个部件需要调整的概率是0.098.
19.(本小题满分12分)
解法一:
(1)证明:在直三棱柱ABC―A1B1C1中,
|