
题目列表(包括答案和解析)
如图,在四棱锥![]() 中,底面
中,底面![]() 是边长为
是边长为![]() 的正方形,
的正方形,![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点,侧面
的中点,侧面![]() ,且
,且![]() .
.
(1)平面![]() 是否垂直于平面
是否垂直于平面![]() ?
?
(2)求三棱锥![]() 的体积.
的体积.

如图,在四棱锥![]() 中,底面
中,底面![]() 是
是
边长为![]() 的菱形,
的菱形,![]() ,
,![]() 平面
平面![]() ,
,
![]() 与平面
与平面![]() 所成角的大小为
所成角的大小为![]() ,
,![]() 为
为![]() 的中点.
的中点.
(1)求四棱锥![]() 的体积;
的体积;
(2)求异面直线![]() 与
与![]() 所成角的大小(结果用
所成角的大小(结果用
反三角函数表示).
如图,在四棱锥![]() 中,底面
中,底面![]() 是边长为
是边长为![]() 的菱形,
的菱形,![]() ,
,
![]() 底面
底面![]() ,
, ![]() ,
,![]() 为
为![]() 的中点,
的中点,![]() 为
为![]() 的中点.
的中点.

(Ⅰ)证明:直线![]() 平面
平面![]() ;
;
(Ⅱ)求异面直线![]() 与
与![]() 所成角的大小;
所成角的大小;
(Ⅲ)求点![]() 到平面
到平面![]() 的距离.
的距离.
如图,在四棱锥![]() 中,底面
中,底面![]() 是边长为2的菱形,且
是边长为2的菱形,且![]() ,
,
![]() 为正三角形,
为正三角形,![]() 为
为![]() 的中点,
的中点,![]() 为棱
为棱![]() 的中点
的中点
(1)求证:![]() 平面
平面![]()
(2)求二面角![]() 的大小
的大小

如图,在四棱锥 中,底面
中,底面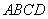 是边长为2的正方形,侧面
是边长为2的正方形,侧面 底面
底面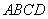 ,且
,且 为等腰直角三角形,
为等腰直角三角形, ,
, 、
、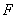 分别为
分别为 、
、 的中点.
的中点.

(1)求证: //平面
//平面 ;
;
(2)若线段 中点为
中点为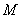 ,求二面角
,求二面角 的余弦值.
的余弦值.
一选择题
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
B
D
A
D
D
B
D
B
A
C
D
C
 提示:10.解:数列
提示:10.解:数列 、
、 都是公差为1的等差数列,其首项分别为
都是公差为1的等差数列,其首项分别为 、
、 ,且
,且 ,
, .设(
.设( ),则
),则

 ,所以
,所以 是等差数列,所以
是等差数列,所以 的前
的前 项和
项和
11.由题 ,消去
,消去 可得:
可得: ,又由题有:
,又由题有: ,由以上条件可得:点
,由以上条件可得:点 的轨迹为如图所示的线段
的轨迹为如图所示的线段 ,而
,而 表示点
表示点 到坐标原点的距离的平方,所以
到坐标原点的距离的平方,所以
12.设点 到左准线的距离为
到左准线的距离为 ,则由双曲线的第二定义有:
,则由双曲线的第二定义有: ,由题有
,由题有 ,所以
,所以 ,又由第一定义
,又由第一定义 (
( 在右支上),所以
在右支上),所以 ,
, ,又由点
,又由点 在右支上,则
在右支上,则 ,
, ,解得:
,解得: ,而
,而 ,所以
,所以
二.填空题
13.  14.
14.  15.
15. 16. 1
16. 1
提示:15.

 ,
, ,
, 
 在
在 单调递减,
单调递减,
 16.如图,设三棱锥得体积为
16.如图,设三棱锥得体积为 ,
, ,当且仅当
,当且仅当 时三棱锥体积最大,过点
时三棱锥体积最大,过点 作
作 ,连接
,连接 ,由题可知
,由题可知 平面
平面 ,由三垂线定理可知
,由三垂线定理可知 为侧面
为侧面 与底面
与底面 成的角,所以
成的角,所以 ,而用等面积法可知:
,而用等面积法可知: ,
, ,所以
,所以 ,代入
,代入 ,得
,得
三.解答题
17.解:(1)取OB中点E,连接ME,NE
 …………………………………………2分
…………………………………………2分
又 …………………………………4分
…………………………………4分
 …………………………………………………………5分
…………………………………………………………5分
(2)连接

 为异面直线
为异面直线 与
与 所成的角(或其补角)…7分
所成的角(或其补角)…7分
由于 ,所以
,所以 ,
, ,
, 为等腰三角形,
为等腰三角形, ……………………………………………………9分
……………………………………………………9分
(3)解法一:连接 ,设点B到平面OCD的距离为
,设点B到平面OCD的距离为 ,
,
由 ,
, ,
, ,
, 为等腰三角形,
为等腰三角形,
 的高为
的高为 ,
, ………11分
………11分
又 ,又
,又

点B到平面OCD的距离为 …………………………………………13分
…………………………………………13分
解法二: 点A和点B到平面OCD的距离相等,取
点A和点B到平面OCD的距离相等,取 的中点P连
的中点P连
接OP,过点作 于点Q,
于点Q, ,又
,又

 又
又  ,
,
线段AQ的长就是点A到平面OCD的距离, ………………………………12分
由题可知: ,
, ,在
,在 中
中 .……13分
.……13分
18.解: 在
在 中,
中,
 ………………………………3分
………………………………3分
 ……5分
……5分
 ……………7分
……………7分
(2)由余弦定理得 ,又由已知和(1)可知:
,又由已知和(1)可知:

 …………………………10分
…………………………10分


 ………………………………13分
………………………………13分
 19.解:(Ⅰ)
19.解:(Ⅰ)
 平面
平面 平面
平面 ,
,
 …………2分
…………2分
在 中,
中, ,
, 为
为 中点
中点
 .……………4分
.……………4分
 平面
平面 ,
, 平面
平面
 平面
平面 .……………6分
.……………6分
(Ⅱ)如图,作 交
交 于
于 点,连接
点,连接 ,
,
由已知得 平面
平面 .
. 是
是 在面
在面 内的射影.
内的射影.
由三垂线定理知 ,
, 为二面角
为二面角 的平面角.……………9分
的平面角.……………9分
过 作
作 交
交 于
于 点,则
点,则 ,
, ,
,
 .在
.在 中,
中, .…………11分
.…………11分
在 中,
中, .
. ,
,
即二面角 为
为 .………………………………13分
.………………………………13分
20.解答:(1) ,
, ,又因为
,又因为 按向量
按向量 平移后得函数
平移后得函数 ……..2分
……..2分
由g(x)图像关于原点对称得g(-x)=-g(x),即 ,
,
 ,
, …………………………………………………...4分
…………………………………………………...4分
由
当 (舍)所以
(舍)所以 …….6分
…….6分
(2)证明:因为
所以 ……………………………………8分
……………………………………8分
故 ……………………………………9分
……………………………………9分
又 ……………………12分
……………………12分
所以 .……………………………………13分
.……………………………………13分
21.解:(I)由已知可得
 ……2分 所以
……2分 所以 …3分 椭圆方程为
…3分 椭圆方程为 ……5分
……5分
(II) ,且定值为
,且定值为 由(I),A2(2,0),B(0,1),且
由(I),A2(2,0),B(0,1),且 //A2B
//A2B
所以直线 的斜率
的斜率 ………………………………6分
………………………………6分
设直线 的方程为
的方程为
 解得:
解得:
 即
即
 ………………………………………………8分
………………………………………………8分

 ……………………9分
……………………9分
又因为




 又
又

 是定值。…………12分
是定值。…………12分
22.(1) (
( 为正整数),
为正整数),
所以数列 的反数列为
的反数列为 的通项
的通项 (
( 为正整数). …………3分
为正整数). …………3分
(2)对于(1)中 ,不等式化为
,不等式化为 .
.
设 ,
,
 ,
,
∴数列 单调递增, 所以,
单调递增, 所以,  ,要使不等式恒成立,只要
,要使不等式恒成立,只要 .
.
∵ ,∴
,∴ ,又
,又 ,
,
所以,使不等式对于任意正整数 恒成立的
恒成立的 的取值范围是
的取值范围是 .…………7分(3)设公共项
.…………7分(3)设公共项 为正整数.
为正整数.
①当 为奇数时,
为奇数时, .
.  ,
,
则 (表示
(表示 是
是 的子数列),
的子数列), .所以
.所以 的前
的前 项和
项和 .
.
② 当 为偶数时,
为偶数时, .
. ,则
,则 ,同样有
,同样有 ,
, .所以
.所以 的前
的前 项和
项和 .
…………12分
.
…………12分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com