
题目列表(包括答案和解析)
设集合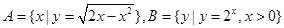 ,则
,则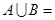
| A.(1,2] | B.[0,+ ) ) |
C.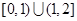 | D.[0,2] |
设集合![]() ,则
,则![]()
A.(1,2] B.[0,+![]() )
)
C.![]() D.[0,2]
D.[0,2]
 ,则
,则
| A.(1,2] | B.[0,+ ) ) |
C. | D.[0,2] |
 A.(不等式选讲选做题)若不等式|x+1|+|x-2|<a无实数解,则a的取值范围是
A.(不等式选讲选做题)若不等式|x+1|+|x-2|<a无实数解,则a的取值范围是
|
 A.(不等式选讲选做题)如果存在实数x使不等式|x+1|-|x-2|<k成立,则实数k的取值范围是
A.(不等式选讲选做题)如果存在实数x使不等式|x+1|-|x-2|<k成立,则实数k的取值范围是| 7 |
1.B 2.D 3.A 4.C 5.C 6.D 7.D 8.B 9.C 10.B
11.A 12.C
1. ,所以选B.
,所以选B.
2. ,所以选D.
,所以选D.
3. ,所以选
,所以选 .
.
4. 或
或 ,所以选C.
,所以选C.
5. ,所以选C.
,所以选C.
6. ,切线斜率
,切线斜率
 ,所以选D.
,所以选D.
7.观察图象 .所以选D.
.所以选D.
8.化为 或
或 ,所以选B.
,所以选B.
9. 与
与 关于
关于 对称,
对称, ,所以选C.
,所以选C.
10.直线 与椭圆
与椭圆 有公共点
有公共点 ,所以选B.
,所以选B.
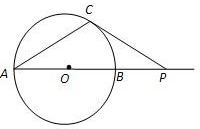
11.如图,设 ,则
,则 ,
,

 ,
,
 ,从而
,从而 ,因此
,因此 与底面所成角的正弦值等于
与底面所成角的正弦值等于 .所以选A.
.所以选A.
12.分类涂色①
只用3种颜色,相对面同色,有1种涂法;② 用4种颜色,有 种涂法;③ 用五种颜色,有
种涂法;③ 用五种颜色,有 种涂法.共有13种涂法.所以选C.
种涂法.共有13种涂法.所以选C.
二、
13.7.由 或
或 (舍去),
(舍去),
 项的余数为
项的余数为 .
.
14.依题设 ,又
,又 ,点
,点 所形成的平面区域为边长为1的正方形,其面积为1.
所形成的平面区域为边长为1的正方形,其面积为1.
15. ,由
,由 ,得
,得
 .
.
16. .
.

如图,可设 ,又
,又 ,
,
 .
.
当 面积最大时,
面积最大时, .点
.点 到直线
到直线 的距离为
的距离为 .
.
三、
17.(1)

由
 得
得 ,
,
 的单调递减区间为
的单调递减区间为 .
.
(2)



 .
.
18.(1) 的所有取值为0.8,0.9,1.0,1.125,1.25,其分布列为
的所有取值为0.8,0.9,1.0,1.125,1.25,其分布列为

0.8
0.9
1.0
1.125
1.25

0.2
0.15
0.35
0.15
0.15
 的所有取值为0.8,0.96,1.0,1,2,1.44,其分布列为
的所有取值为0.8,0.96,1.0,1,2,1.44,其分布列为

0.8
0.96
1.0
1.2
1.44

0.3
0.2
0.18
0.24
0.08
(2)设实施方案一、方案二两年后超过危机前出口额的概率为 ,
, ,则
,则

∴实施方案二两年后超过危机前出口额的概率更大.
(3)方案一、方案二的预计利润为 、
、 ,则
,则

10
15
20

0.35
0.35
0.3

10
15
20

0. 5
0.18
0.32


∴实施方案一的平均利润更大
19.(1)设 与
与 交于点
交于点 .
.



从而 ,即
,即 ,又
,又 ,且
,且
 平面
平面 为正三角形,
为正三角形, 为
为 的中点,
的中点,
 ,且
,且 ,因此,
,因此, 平面
平面 .
.
(2) 平面
平面 ,∴平面
,∴平面 平面
平面 又
又 ,∴平面
,∴平面 平面
平面
设 为
为 的中点,连接
的中点,连接 ,则
,则 ,
,
 平面
平面 ,过点
,过点 作
作 ,连接
,连接 ,则
,则 .
.
 为二面角
为二面角 的平面角.
的平面角.
在 中,
中, .
.
又 .
.
20.(1)由 ,得
,得 ,则
,则
又 为正整数,
为正整数,

 ,故
,故 .
.
(2)

∴当 或
或 时,
时, 取得最小值
取得最小值 .
.
21.(1)由 得
得
∴椭圆 的方程为:
的方程为: .
.
(2)由 得
得 ,
,

又
设直线 的方程为:
的方程为:
由 得
得


由此得 . ①
. ①
设 与椭圆
与椭圆 的交点为
的交点为 ,则
,则
www.ks5u.com由 得
得
 ,整理得
,整理得
 ,整理得
,整理得
 时,上式不成立,
时,上式不成立, ②
②
由式①、②得
 或
或
∴ 取值范围是
取值范围是 .
.
22.(1)由 得
得
令 ,则
,则
当 时,
时, 在
在 上单调递增.
上单调递增.

 的取值范围是
的取值范围是 .
.
(2)
则
① 当 时,
时, 是减函数.
是减函数.
 时,
时, 是增函数.
是增函数.
② 当 时,
时, 是增函数.
是增函数.
综上;当 时,增区间为
时,增区间为 ,,减区间为
,,减区间为 ;
;
当 时,增区间为
时,增区间为 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com