
题目列表(包括答案和解析)
| a |
| b |
| c |
| b |
| c |
| d |
| a |
| b |
| c |
| d |
| a |
| a |
| MP |
| MA |
| MB |
| OP |
| OA |
| OB |
| OC |
已知椭圆 的长轴在
的长轴在 轴上,且焦距为4,则
轴上,且焦距为4,则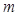 等于( )
等于( )
A.4 B.5 C.7 D.8
已知椭圆的长轴长是短轴长的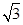 倍,则椭圆的离心率等于
倍,则椭圆的离心率等于
A. B.
B.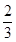 C.
C.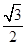 D.
D.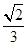
已知椭圆的长轴长是短轴长的3倍,则椭圆的离心率等于( ).
A. B.
B.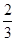 C.
C.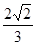 D.
D.
已知椭圆 的长轴长为10,离心率
的长轴长为10,离心率 ,则椭圆的方程是( )
,则椭圆的方程是( )
A. 或
或 B.
B. 或
或
C. 或
或 D.
D. 或
或
一、选择题
1.C 2.D 3.B 4.B 5.C 6.D 7. B 8.C 9.D 10.B11.A 12.B
二、填空题
13.%20数学文科.files/image247.gif) 14.-
14.-%20数学文科.files/image249.gif) 15.[-1,2] 16.①④
15.[-1,2] 16.①④
三、解答题
17.解:(Ⅰ)由%20数学文科.files/image163.gif) ,
,%20数学文科.files/image252.gif) ,得
,得%20数学文科.files/image254.gif) .
.
∴%20数学文科.files/image256.gif) .
.
于是%20数学文科.files/image258.gif) .
.
(Ⅱ)由%20数学文科.files/image167.gif) ,得
,得%20数学文科.files/image260.gif) .
.
又∵%20数学文科.files/image165.gif) ,
,
∴%20数学文科.files/image262.gif) .
.
由%20数学文科.files/image264.gif) ,得
,得
%20数学文科.files/image266.gif)
%20数学文科.files/image268.gif)
%20数学文科.files/image270.gif)
∴%20数学文科.files/image272.gif) .
.
18.(Ⅰ)证明:在直四棱柱%20数学文科.files/image178.gif) 中,
中,
连结%20数学文科.files/image275.gif) ,
,
%20数学文科.files/image277.gif) ,
,
%20数学文科.files/image279.gif) 四边形
四边形%20数学文科.files/image281.gif) 是正方形.
是正方形.
%20数学文科.files/image283.gif) .
.
%20数学文科.files/image284.gif) 又
又%20数学文科.files/image286.gif) ,
,%20数学文科.files/image288.gif) ,
,
%20数学文科.files/image290.gif) 平面
平面%20数学文科.files/image281.gif) ,
,
%20数学文科.files/image293.gif) 平面
平面%20数学文科.files/image281.gif) ,
,
%20数学文科.files/image296.gif) .
.
%20数学文科.files/image298.gif) 平面
平面%20数学文科.files/image300.gif) ,
,
且%20数学文科.files/image302.gif) ,
,
%20数学文科.files/image304.gif) 平面
平面%20数学文科.files/image300.gif) ,
,
又%20数学文科.files/image307.gif) 平面
平面%20数学文科.files/image300.gif) ,
,
%20数学文科.files/image310.gif) .
.
(Ⅱ)连结%20数学文科.files/image312.gif) ,连结
,连结%20数学文科.files/image314.gif) ,
,
设%20数学文科.files/image316.gif) ,
,
%20数学文科.files/image318.gif) ,连结
,连结%20数学文科.files/image320.gif) ,
,
%20数学文科.files/image322.gif) 平面
平面%20数学文科.files/image324.gif) 平面
平面%20数学文科.files/image326.gif) ,
,
要使%20数学文科.files/image191.gif) 平面
平面%20数学文科.files/image193.gif) ,
,
须使%20数学文科.files/image330.gif) ,
,
又%20数学文科.files/image332.gif) 是
是%20数学文科.files/image312.gif) 的中点.
的中点.
%20数学文科.files/image335.gif) 是
是%20数学文科.files/image314.gif) 的中点.
的中点.
又易知%20数学文科.files/image338.gif) ,
,
%20数学文科.files/image340.gif) .
.
即%20数学文科.files/image186.gif) 是
是%20数学文科.files/image188.gif) 的中点.
的中点.
综上所述,当%20数学文科.files/image186.gif) 是
是%20数学文科.files/image188.gif) 的中点时,可使
的中点时,可使%20数学文科.files/image191.gif) 平面
平面%20数学文科.files/image193.gif) .
.
19.解:(Ⅰ)
更 爱 好 体 育
更 爱 好 文 娱
合 计
男 生
15
10
25
女 生
5
10
15
合 计
20
20
40
…………………………………5分
(Ⅱ)恰好是一男一女的概率是:%20数学文科.files/image348.gif)
(Ⅲ)%20数学文科.files/image350.gif)
%20数学文科.files/image352.gif)
%20数学文科.files/image354.gif)
而%20数学文科.files/image356.gif)
∴有85%的把握可以认为性别与是否更喜欢体育有关系。
20.解:(Ⅰ)设等比数列%20数学文科.files/image358.gif) 的公比为
的公比为%20数学文科.files/image360.gif)
由%20数学文科.files/image362.gif) ,得
,得%20数学文科.files/image364.gif) ,从而
,从而%20数学文科.files/image366.gif) ,
,%20数学文科.files/image368.gif) ,
,%20数学文科.files/image370.gif) .
.
因为%20数学文科.files/image372.gif) 成等差数列,所以
成等差数列,所以%20数学文科.files/image374.gif) ,
,
即%20数学文科.files/image376.gif) ,
,%20数学文科.files/image378.gif) .
.
所以%20数学文科.files/image380.gif) .故
.故%20数学文科.files/image382.gif) .
.
(Ⅱ)%20数学文科.files/image384.gif)
21.解:(Ⅰ)%20数学文科.files/image386.gif) ,由已知
,由已知%20数学文科.files/image388.gif) ,
,
即%20数学文科.files/image390.gif) 解得
解得%20数学文科.files/image392.gif)
%20数学文科.files/image394.gif) ,
,%20数学文科.files/image396.gif) ,
,%20数学文科.files/image398.gif) ,
,%20数学文科.files/image400.gif) .
.
(Ⅱ)令%20数学文科.files/image402.gif) ,即
,即%20数学文科.files/image404.gif) ,
,
%20数学文科.files/image406.gif) ,
,%20数学文科.files/image408.gif) 或
或%20数学文科.files/image410.gif) .
.
又%20数学文科.files/image402.gif) 在区间
在区间%20数学文科.files/image413.gif) 上恒成立,
上恒成立,%20数学文科.files/image415.gif) .
.
22.解:(Ⅰ)设椭圆的半焦距为%20数学文科.files/image417.gif) ,依题意
,依题意%20数学文科.files/image419.gif)
%20数学文科.files/image421.gif) ,
,%20数学文科.files/image279.gif) 所求椭圆方程为
所求椭圆方程为%20数学文科.files/image424.gif) .
.
(Ⅱ)设%20数学文科.files/image426.gif) ,
,%20数学文科.files/image428.gif) .
.
(1)当%20数学文科.files/image430.gif) 轴时,
轴时,%20数学文科.files/image432.gif) .
.
(2)当%20数学文科.files/image434.gif) 与
与%20数学文科.files/image127.gif) 轴不垂直时,
轴不垂直时,
设直线%20数学文科.files/image434.gif) 的方程为
的方程为%20数学文科.files/image438.gif) .
.
由已知%20数学文科.files/image440.gif) ,得
,得%20数学文科.files/image442.gif) .
.
把%20数学文科.files/image438.gif) 代入椭圆方程,整理得
代入椭圆方程,整理得%20数学文科.files/image445.gif) ,
,
%20数学文科.files/image447.gif) ,
,%20数学文科.files/image449.gif) .
.
%20数学文科.files/image451.gif)
%20数学文科.files/image453.gif)
%20数学文科.files/image455.gif)
%20数学文科.files/image457.gif) .
.
当且仅当%20数学文科.files/image459.gif) ,即
,即%20数学文科.files/image461.gif) 时等号成立.当
时等号成立.当%20数学文科.files/image463.gif) 时,
时,%20数学文科.files/image432.gif) ,
,
综上所述%20数学文科.files/image466.gif) .
.
%20数学文科.files/image279.gif) 当
当%20数学文科.files/image469.gif) 最大时,
最大时,%20数学文科.files/image471.gif) 面积取最大值
面积取最大值%20数学文科.files/image473.gif) .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com