
题目列表(包括答案和解析)
()中学数学中存在许多关系,比如“相等关系”、“平行关系”等等.如果集合A中元素之间的一个关系“-”满足以下三个条件:
(1)自反性:对于任意a∈A,都有a-a;
(2)对称性:对于a,b∈A,若a-b,则有b-a;
(3)传递性:对于a,b,c∈A,若a-b,b-c,则有a-c.
则称“-”是集合A的一个等价关系.例如:“数的相等”是等价关系,而“直线的平行”不是等价关系(自反性不成立).请你再列出两个等价关系: .
(Ⅰ)已知函数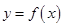 ,若存在
,若存在 ,使得
,使得 ,则称
,则称 是函数
是函数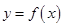 的一个不动点,设二次函数
的一个不动点,设二次函数 .
.
(Ⅰ) 当 时,求函数
时,求函数 的不动点;
的不动点;
(Ⅱ) 若对于任意实数 ,函数
,函数 恒有两个不同的不动点,求实数
恒有两个不同的不动点,求实数 的取值范围;
的取值范围;
(Ⅲ) 在(Ⅱ)的条件下,若函数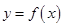 的图象上
的图象上 两点的横坐标是函数
两点的横坐标是函数 的不动点,且直线
的不动点,且直线 是线段
是线段 的垂直平分线,求实数
的垂直平分线,求实数 的取值范围.
的取值范围.
(Ⅰ)已知函数 ,若存在
,若存在 ,使得
,使得 ,则称
,则称 是函数
是函数 的一个不动点,设二次函数
的一个不动点,设二次函数 .
.
(Ⅰ) 当 时,求函数
时,求函数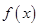 的不动点;
的不动点;
(Ⅱ) 若对于任意实数 ,函数
,函数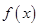 恒有两个不同的不动点,求实数
恒有两个不同的不动点,求实数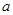 的取值范围;
的取值范围;
(Ⅲ) 在(Ⅱ)的条件下,若函数 的图象上
的图象上 两点的横坐标是函数
两点的横坐标是函数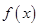 的不动点,且直线
的不动点,且直线 是线段
是线段 的垂直平分线,求实数
的垂直平分线,求实数 的取值范围.
的取值范围.
 ,若存在
,若存在 ,使得
,使得 ,则称
,则称 是函数
是函数 的一个不动点,设二次函数
的一个不动点,设二次函数 .
.  时,求函数
时,求函数 的不动点;
的不动点; ,函数
,函数 恒有两个不同的不动点,求实数
恒有两个不同的不动点,求实数 的取值范围;
的取值范围; 的图象上
的图象上 两点的横坐标是函数
两点的横坐标是函数 的不动点,且直线
的不动点,且直线 是线段
是线段 的垂直平分线,求实数
的垂直平分线,求实数 的取值范围.
的取值范围.若函数 对任意的
对任意的 ,均有
,均有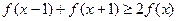 ,则称函数
,则称函数 具有性质
具有性质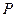 .
.
(Ⅰ)判断下面两个函数是否具有性质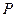 ,并说明理由.
,并说明理由.
① ; ②
; ②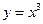 .
.
(Ⅱ)若函数 具有性质
具有性质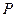 ,且
,且 (
(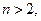
 ),
),
求证:对任意 有
有 ;
;
(Ⅲ)在(Ⅱ)的条件下,是否对任意 均有
均有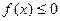 .若成立给出证明,若不成立给出反例.
.若成立给出证明,若不成立给出反例.
一、选择题:
1. 答案:C.  {x | x≥0},故选C.
{x | x≥0},故选C.
2.C
3. (理)对于 中,当n=6时,有
中,当n=6时,有 所以第25项是7.选C.
所以第25项是7.选C.
4.D
5.A. ∵
= ,
,
∴根据题意作出函数图象即得.选A.
6. 答案:D.当x=1时,y=m ,由图形易知m<0, 又函数是减函数,所以0<n<1,故选D.
7.A
8.C
二、填空题:
9.810
10.答案: .
.



11. 答案: .
.

12.
13. (2)、(3)
14.
15.(本题满分 分)
分)
已知 ,
,
(Ⅰ)求 的值;
的值;
(Ⅱ)求 的值.
的值.
解:(Ⅰ)由 ,
,  ,
………………………2分
,
………………………2分
 .
…………………5分
.
…………………5分
(Ⅱ) 原式= 

 …………………10分
…………………10分


 .
…………………12分
.
…………………12分
16.(本题满分 分)
分)
在一个盒子中,放有标号分别为 ,
, ,
, 的三张卡片,现从这个盒子中,有放回地先后抽得两张卡片的标号分别为
的三张卡片,现从这个盒子中,有放回地先后抽得两张卡片的标号分别为 、
、 ,记
,记 .
.
(Ⅰ)求随机变量 的最大值,并求事件“
的最大值,并求事件“ 取得最大值”的概率;
取得最大值”的概率;
(Ⅱ)求随机变量 的分布列和数学期望.
的分布列和数学期望.
解:(Ⅰ) 、
、 可能的取值为
可能的取值为 、
、 、
、 ,
,
 ,
, ,
,
 ,且当
,且当 或
或 时,
时, .
……………3分
.
……………3分
因此,随机变量 的最大值为
的最大值为 .
.
 有放回抽两张卡片的所有情况有
有放回抽两张卡片的所有情况有 种,
种,
 .
.
答:随机变量 的最大值为
的最大值为 ,事件“
,事件“ 取得最大值”的概率为
取得最大值”的概率为 . ………5分
. ………5分
(Ⅱ) 的所有取值为
的所有取值为 .
.
 时,只有
时,只有 这一种情况,
这一种情况,
 时,有
时,有 或
或 或
或 或
或 四种情况,
四种情况,
 时,有
时,有 或
或 两种情况.
两种情况.
 ,
, ,
, .
…………11分
.
…………11分
则随机变量 的分布列为:
的分布列为:










因此,数学期望 . ……………………13分
. ……………………13分
17.(本题满分 分)
分)
如图,已知正三棱柱 ―
― 的底面边长是
的底面边长是 ,
, 是侧棱
是侧棱 的中点,直线
的中点,直线 与侧面
与侧面 所成的角为
所成的角为 .
.
(Ⅰ)求此正三棱柱的侧棱长;(Ⅱ) 求二面角 的大小;
的大小;
(Ⅲ)求点 到平面
到平面 的距离.
的距离.
 解:(Ⅰ)设正三棱柱
解:(Ⅰ)设正三棱柱 ―
― 的侧棱长为
的侧棱长为 .取
.取 中点
中点 ,连
,连 .
.
 是正三角形,
是正三角形, .
.
又底面 侧面
侧面 ,且交线为
,且交线为 .
.
 侧面
侧面 .
.
连 ,则直线
,则直线 与侧面
与侧面 所成的角为
所成的角为 . ……………2分
. ……………2分
在 中,
中, ,解得
,解得 . …………3分
. …………3分
 此正三棱柱的侧棱长为
此正三棱柱的侧棱长为 .
……………………4分
.
……………………4分
注:也可用向量法求侧棱长.
(Ⅱ)解法1:过 作
作 于
于 ,连
,连 ,
,
 侧面
侧面

 .
.
 为二面角
为二面角 的平面角.
……………………………6分
的平面角.
……………………………6分
在 中,
中, ,又
,又
 ,
, 
 .
.
又
 在
在 中,
中, .
…………………………8分
.
…………………………8分
故二面角 的大小为
的大小为 .
…………………………9分
.
…………………………9分
解法2:(向量法,见后)
(Ⅲ)解法1:由(Ⅱ)可知, 平面
平面 ,
, 平面
平面 平面
平面 ,且交线为
,且交线为 ,
, 过
过 作
作 于
于 ,则
,则 平面
平面 .
…………10分
.
…………10分
在 中,
中, .
…………12分
.
…………12分

 为
为 中点,
中点, 点
点 到平面
到平面 的距离为
的距离为 . …………13分
. …………13分
解法2:(思路)取 中点
中点 ,连
,连 和
和 ,由
,由
 ,易得平面
,易得平面 平面
平面 ,且交线为
,且交线为 .过点
.过点 作
作 于
于 ,则
,则 的长为点
的长为点 到平面
到平面 的距离.
的距离.
解法3:(思路)等体积变换:由 可求.
可求.
解法4:(向量法,见后)
题(Ⅱ)、(Ⅲ)的向量解法:
 (Ⅱ)解法2:如图,建立空间直角坐标系
(Ⅱ)解法2:如图,建立空间直角坐标系 .
.
则 .
.
设
 为平面
为平面 的法向量.
的法向量.
由 得
得
 .
.
 取
取 …………6分
…………6分
又平面 的一个法向量
的一个法向量 …………7分
…………7分

 . …………8分
. …………8分
结合图形可知,二面角 的大小为
的大小为 .
…………9分
.
…………9分
(Ⅲ)解法4:由(Ⅱ)解法2,
 …………10分
…………10分
 点
点 到平面
到平面 的距离
的距离
 =
= .13分
.13分
18. (本小题满分14分)
一束光线从点 出发,经直线
出发,经直线 上一点
上一点 反射后,恰好穿过点
反射后,恰好穿过点 .
.
(Ⅰ)求点 关于直线
关于直线 的对称点
的对称点 的坐标;
的坐标;
(Ⅱ)求以 、
、 为焦点且过点
为焦点且过点 的椭圆
的椭圆 的方程;
的方程;
(Ⅲ)设直线 与椭圆
与椭圆 的两条准线分别交于
的两条准线分别交于 、
、 两点,点
两点,点 为线段
为线段 上的动点,求点
上的动点,求点 到
到 的距离与到椭圆
的距离与到椭圆 右准线的距离之比的最小值,并求取得最小值时点
右准线的距离之比的最小值,并求取得最小值时点 的坐标.
的坐标.
解:(Ⅰ)设 的坐标为
的坐标为 ,则
,则 且
且 .……2分
.……2分
解得 , 因此,点
, 因此,点  的坐标为
的坐标为 . …………………4分
. …………………4分
(Ⅱ) ,根据椭圆定义,
,根据椭圆定义,
得
 ,……………5分
,……………5分
 ,
, .
.
∴所求椭圆方程为 .
………………………………7分
.
………………………………7分
(Ⅲ) ,
, 椭圆的准线方程为
椭圆的准线方程为 . …………………………8分
. …………………………8分
设点 的坐标为
的坐标为
 ,
, 表示点
表示点 到
到 的距离,
的距离, 表示点
表示点 到椭圆的右准线的距离.
到椭圆的右准线的距离.
则 ,
, .
.
 ,
……………………………10分
,
……………………………10分
令
 ,则
,则 ,
,
 当
当 ,
, ,
,
 ,
, .
.
∴  在
在 时取得最小值.
………………………………13分
时取得最小值.
………………………………13分
因此, 最小值=
最小值= ,此时点
,此时点 的坐标为
的坐标为 .…………14分
.…………14分
注: 的最小值还可以用判别式法、换元法等其它方法求得.
的最小值还可以用判别式法、换元法等其它方法求得.
说明:求得的点
 即为切点
即为切点 ,
, 的最小值即为椭圆的离心率.
的最小值即为椭圆的离心率.
19.(本题满分 分)
分)
已知数列 满足:
满足: 且
且 ,
, .
.
(Ⅰ)求 ,
, ,
, ,
, 的值及数列
的值及数列 的通项公式;
的通项公式;
(Ⅱ)设 ,求数列
,求数列 的前
的前 项和
项和 ;
;
解:(Ⅰ)经计算 ,
, ,
, ,
, .
.
当 为奇数时,
为奇数时, ,即数列
,即数列 的奇数项成等差数列,
的奇数项成等差数列,
 ;
;
当 为偶数,
为偶数, ,即数列
,即数列 的偶数项成等比数列,
的偶数项成等比数列,
 .
.
因此,数列 的通项公式为
的通项公式为 .
.
(Ⅱ)
 ,
,
 ……(1)
……(1)
 …(2)
…(2)
(1)、(2)两式相减,
得

 .
.
 .
.
20.(本题满分 分)
分)
已知函数 和点
和点 ,过点
,过点 作曲线
作曲线 的两条切线
的两条切线 、
、 ,切点分别为
,切点分别为 、
、 .
.
(Ⅰ)设 ,试求函数
,试求函数 的表达式;
的表达式;
(Ⅱ)是否存在 ,使得
,使得 、
、 与
与 三点共线.若存在,求出
三点共线.若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(Ⅲ)在(Ⅰ)的条件下,若对任意的正整数 ,在区间
,在区间 内总存在
内总存在 个实数
个实数
 ,
, ,使得不等式
,使得不等式 成立,求
成立,求 的最大值.
的最大值.
解:(Ⅰ)设 、
、 两点的横坐标分别为
两点的横坐标分别为 、
、 ,
,

 ,
,  切线
切线 的方程为:
的方程为: ,
,
又 切线
切线 过点
过点 ,
,  有
有 ,
,
即 , ………………………………………………(1) …… 2分
, ………………………………………………(1) …… 2分
同理,由切线 也过点
也过点 ,得
,得 .…………(2)
.…………(2)
由(1)、(2),可得 是方程
是方程 的两根,
的两根,
 ………………( * )
……………………… 4分
………………( * )
……………………… 4分


 ,
,
把( * )式代入,得 ,
,
因此,函数 的表达式为
的表达式为 . ……………………5分
. ……………………5分
(Ⅱ)当点 、
、 与
与 共线时,
共线时, ,
,
 =
= ,
,
即 =
= ,化简,得
,化简,得 ,
,
 ,
, . ………………(3) …………… 7分
. ………………(3) …………… 7分
把(*)式代入(3),解得 .
.
 存在
存在 ,使得点
,使得点 、
、 与
与 三点共线,且
三点共线,且  . ……………………9分
. ……………………9分
(Ⅲ)解法 :易知
:易知 在区间
在区间 上为增函数,
上为增函数,


 ,
,
则 .
.
依题意,不等式 对一切的正整数
对一切的正整数 恒成立, …………11分
恒成立, …………11分
 ,
,
即 对一切的正整数
对一切的正整数
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com