（2013•顺义区二模）问题：如果存在一组平行线a∥b∥c，请你猜想是否可以作等边三角形ABC使其三个顶点分别在a、b、c上？
小明同学的解答如下：如图1所示，过点A作AM⊥b于M，作∠MAN=60°，且AN=AM，过点N作CN⊥AN交直线c于点C，在直线b上取点B使BM=CN，则△ABC为所求．

（1）请你参考小明的作法，在图2中作一个等腰直角三角形DEF使其三个顶点分别在a、b、c上，点D为直角顶点；
（2）若直线a、b之间的距离为1，b、c之间的距离为2，则在图2中，S_△DEF=，在图1中AC=．

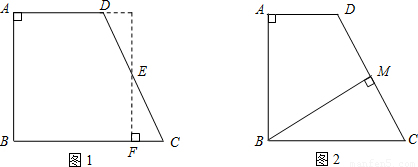
（2012•宁德质检）在数学“综合与实践”课中，陈老师要求同学们制作一张直角梯形纸片ABCD，要求梯形的上底AD=3cm，下底BC=5cm．探索：当直角梯形ABCD的高AB是多少厘米时，将该梯形沿某一直线剪成两部分后，能拼成一个既不重叠又无空隙的特殊几何图形．
（1）如图1，小颖过腰CD的中点E作EF⊥BC于F，沿EF将梯形剪切后，拼成正方形．求小颖所制作的直角梯形的高AB是多少厘米？
（2）如图2，小亮过点B作BM⊥CD于M，沿BM将梯形剪切后，拼成直角三角形．请在答题卡的相应位置补全拼后的一种直角三角形草图，并求小亮所制作的直角梯形的高AB是多少厘米？
（3）探索当直角梯形的高AB是多少厘米时，将该梯形沿某一直线剪成两部分后，能拼成一个不是正方形的菱形．请在答题卡的相应位置画出两种不同剪切、拼图方法的草图，并直接写出原直角梯形的高AB．

在△ABC中，AB=AC，CD⊥AB交AB于点D，将三角板MNP按图甲的位置摆放，使三角板的一条直角边MP与AC边在一条直线上，当另一条直角边MN恰好经过点B时，易证：BM=CD．

（1）当三角板沿AC方向平移到图乙的位置（一条直角边MP仍与AC边在同一直线上，另一条直角边MN交BC边于点E，过点E作EF⊥AB于点F）时，请你猜想线段EF、EM、CD之间的数量关系，并证明你的猜想；
（2）当三角板沿AC方向继续平移到图丙所示的位置（线段NM的延长线与BC的延长线交于点E）时，线段EF、EM、CD之间的又有怎样的数量关系？请写出你的猜想，不需证明．