
题目列表(包括答案和解析)
某班从6名班干部中(其中男生4人,女生2人),任选3人参加学校的义务劳动.
(1)设所选3人中女生人数为ξ,求ξ的分布列;
(2)设“男生甲被选中”为事件A,“女生乙被选中”为事件B,求P(B)和P(B|A).
(本题满分16分)
 2010年上海世博会某国要建一座八边形的展馆区,它的主体造型的平面图是由两个相同的矩形
2010年上海世博会某国要建一座八边形的展馆区,它的主体造型的平面图是由两个相同的矩形 和
和 构成的面积为200
构成的面积为200 的十字型地域,计划在正方形
的十字型地域,计划在正方形 上建一座“观景花坛”,造价为4200元
上建一座“观景花坛”,造价为4200元 ,在四个相同的矩形上(图中阴影部分)铺花岗岩地坪,造价为210元
,在四个相同的矩形上(图中阴影部分)铺花岗岩地坪,造价为210元 ,再在四个空角(如
,再在四个空角(如 等)上铺草坪,造价为80元
等)上铺草坪,造价为80元 .设
.设 长为
长为 ,
, 长为
长为 .
.
(1)试找出 与
与 满足的等量关系式;
满足的等量关系式;
(2)设总造价为 元,试建立
元,试建立 与
与 的函数关系;
的函数关系;
(3)若总造价 不超过138000元,求
不超过138000元,求 长
长 的取值范围.
的取值范围.

(1)设λ=3为事件B,求事件B的概率P1;
(2)设λ不大于3为事件C,求事件C的概率P2.
 ,被乙小组攻克的概率为
,被乙小组攻克的概率为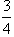 ,
, -a)x在定义域内单调递减”为事件A,求事件A发生的概率。
-a)x在定义域内单调递减”为事件A,求事件A发生的概率。(本题满分16分)
 2010年上海世博会某国要建一座八边形的展馆区,它的主体造型的平面图是由两个相同的矩形
2010年上海世博会某国要建一座八边形的展馆区,它的主体造型的平面图是由两个相同的矩形![]() 和
和![]() 构成的面积为200
构成的面积为200![]() 的十字型地域,计划在正方形
的十字型地域,计划在正方形![]() 上建一座“观景花坛”,造价为4200元
上建一座“观景花坛”,造价为4200元![]() ,在四个相同的矩形上(图中阴影部分)铺花岗岩地坪,造价为210元
,在四个相同的矩形上(图中阴影部分)铺花岗岩地坪,造价为210元![]() ,再在四个空角(如
,再在四个空角(如![]() 等)上铺草坪,造价为80元
等)上铺草坪,造价为80元![]() .设
.设![]() 长为
长为![]() ,
,![]() 长为
长为![]() .
.
(1)试找出![]() 与
与![]() 满足的等量关系式;
满足的等量关系式;
(2)设总造价为![]() 元,试建立
元,试建立![]() 与
与![]() 的函数关系;
的函数关系;
 (3)若总造价
(3)若总造价![]() 不超过138000元,求
不超过138000元,求![]() 长
长![]() 的取值范围.
的取值范围.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com