练习册

  • 练习册
  • 试题
    本小题满分10分)选修4-1:几何证明选讲 如图.已知的两条角平分线和相交于H..F在上. 且. (Ⅰ)证明:B,D,H,E四点共圆: (Ⅱ)证明:平分. 解:(Ⅰ)在△ABC中.因为∠B=60°. 所以∠BAC+∠BCA=120°. 因为AD.CE是角平分线. 所以∠HAC+∠HCA=60°. 故∠AHC=120°. 于是∠EHD=∠AHC=120°. 因为∠EBD+∠EHD=180°. 所以B,D,H,E四点共圆. (Ⅱ)连结BH,则BH为∠ABC的平分线.得∠HBD=30° 由(Ⅰ)知B,D,H,E四点共圆. 所以∠CED=∠HBD=30°. 又∠AHE=∠EBD=60°.由已知可得EF⊥AD. 可得∠CEF=30°. 所以CE平分∠DEF. 【查看更多】

     

    题目列表(包括答案和解析)

    （22、23、24三题中任选一题作答，如果多做，则按所做的的第一题记分）
    (本小题满分10分)选修4—5：不等式选讲
    设函数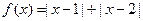
    (1)求不等式的解集；
    (2)若不等式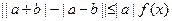（，，）恒成立，求实数的范围．

    查看答案和解析>>

    （22、23、24三题中任选一题作答，如果多做，则按所做的的第一题记分）
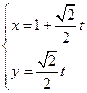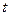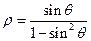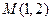    (本小题满分10分)选修4—4：坐标系与参数方程已知直线的参数方程为（为参数），曲线C的极坐标方程是，以极点为原点，极轴为轴正方向建立直角坐标系，点，直线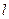与曲线C交于A、B两点．
    (1)写出直线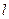的极坐标方程与曲线C的普通方程；
    (2) 线段MA，MB长度分别记为|MA|，|MB|，求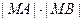的值．

    查看答案和解析>>

    （22、23、24三题中任选一题作答，如果多做，则按所做的的第一题记分）(本小题满分10分)选修4—1：几何证明选讲
    如图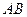，是⊙的直径，弦CA、BD的延长线相交于点E，EF垂直BA的延长线于点F．

    求证：(1)；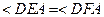
    (2)．

    查看答案和解析>>

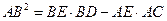    (本小题满分10分)选修4－1：几何证明选讲

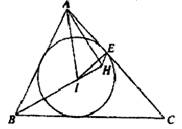
    如图，锐角△ABC的内心为I，过点A作直线BI的垂线，垂足为H，点E为内切圆I与边CA的切点.

    (Ⅰ)求证：四点A，I，H，E共圆；

    (Ⅱ)若∠C＝50°，求∠IEH的度数.

     

    查看答案和解析>>

    (本小题满分10分)选修4-1几何证明选讲

    已知ΔABC中AB=AC，D为ΔABC外接圆劣弧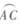上的点(不与点A、C重合），延长BD至E，延长交BC的延长线于F .

    (I )求证：；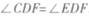

    (II)求证：AB.AC.DF=AD.FC.FB.

     

    查看答案和解析>>


    同步练习册答案