
题目列表(包括答案和解析)
 探究光的反射规律时,在平面镜的上方垂直放置一块光屏,光屏由可以绕ON折转的E、F两块板组成.让一束光贴着光屏左侧的E板沿AO方向射到O点,在右侧F板上能看到反射光线OB.实验时从光屏前不同的方向都能看到光的传播路径,这是因为光在光屏上发生了
探究光的反射规律时,在平面镜的上方垂直放置一块光屏,光屏由可以绕ON折转的E、F两块板组成.让一束光贴着光屏左侧的E板沿AO方向射到O点,在右侧F板上能看到反射光线OB.实验时从光屏前不同的方向都能看到光的传播路径,这是因为光在光屏上发生了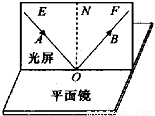
 探究光的反射规律时,在平面镜的上方垂直放置一块光屏,光屏由可以绕ON折转的E、F两块板组成.让一束光贴着光屏左侧的E板沿AO方向射到O点,在右侧F板上能看到反射光线OB.实验时从光屏前不同的方向都能看到光的传播路径,这是因为光在光屏上发生了________ (填“镜面”或“漫”)反射.改变入射光的入射方向,可以看到反射角与入射角________.若将F板向后折转一定的角度,则在F板上不能看到反射光,此时反射光线和入射光线 (填“在”或“不在”)________同一平面内.
探究光的反射规律时,在平面镜的上方垂直放置一块光屏,光屏由可以绕ON折转的E、F两块板组成.让一束光贴着光屏左侧的E板沿AO方向射到O点,在右侧F板上能看到反射光线OB.实验时从光屏前不同的方向都能看到光的传播路径,这是因为光在光屏上发生了________ (填“镜面”或“漫”)反射.改变入射光的入射方向,可以看到反射角与入射角________.若将F板向后折转一定的角度,则在F板上不能看到反射光,此时反射光线和入射光线 (填“在”或“不在”)________同一平面内. 如图,探究光的反射规律时,在平面镜的上方垂直放置一块光屏,光屏由可以绕ON折转的E、F两块板组成.让一束光贴着光屏左侧的E板沿AO方向射到O点,在右侧F板上能看到反射光OB.实验时从光屏前不同的方向都能看到光的传播路径,这是因为光在光屏上发生了
如图,探究光的反射规律时,在平面镜的上方垂直放置一块光屏,光屏由可以绕ON折转的E、F两块板组成.让一束光贴着光屏左侧的E板沿AO方向射到O点,在右侧F板上能看到反射光OB.实验时从光屏前不同的方向都能看到光的传播路径,这是因为光在光屏上发生了 如图,探究光的反射规律时,在平面镜的上方垂直放置一块光屏,光屏由可以绕ON折转的E、F两块板组成.让一束光贴着光屏左侧的E板沿AO方向射到O点,在右侧F板上能看到反射光线OB.
如图,探究光的反射规律时,在平面镜的上方垂直放置一块光屏,光屏由可以绕ON折转的E、F两块板组成.让一束光贴着光屏左侧的E板沿AO方向射到O点,在右侧F板上能看到反射光线OB.一、选择题:(每小题5分,.files/image303.gif) 共60分)
共60分)
1.C 2.D 3.D 4. 文C理B 5.B 6.C 7. 文C理A
8.C 9.A 10.D 11.A. 12. 文B理D
二、填空题:(每小题4分,共16分)
13..files/image305.gif) ;
14. 2 15.
;
14. 2 15..files/image307.gif) 或者
或者.files/image309.gif) ; 16.③④
; 16.③④
三、解答题:(共74分)
17.解:设.files/image311.gif) 关于
关于.files/image048.gif) 轴对称的点
轴对称的点.files/image314.gif) 为,易知点
为,易知点.files/image314.gif) 的坐标为(-2,-3)。 ……2分
的坐标为(-2,-3)。 ……2分
∵反射光线.files/image317.gif) 的反向延长线必过
的反向延长线必过.files/image314.gif) (-2,-3),
……2分
(-2,-3),
……2分
又直线.files/image317.gif) 与已知直线
与已知直线.files/image320.gif) 平行,∴
平行,∴.files/image322.gif) 。
……2分
。
……2分
∴直线.files/image317.gif) 的方程为
的方程为.files/image324.gif) 。
……2分
。
……2分
由两条平行直线间的距离公式,可得.files/image326.gif) 。
……3分
。
……3分
∴所求的直线.files/image317.gif) 和直线
和直线.files/image320.gif) 的距离为
的距离为.files/image328.gif) 。
……1分
。
……1分
.files/image330.jpg) 18.证明:
18.证明:
.files/image332.jpg)
∵AM为平面PCD的斜线,MN为斜线AM在平面PCD的射影, ……2分
又MN⊥PC交PC于M,
∴由三垂线定理,可知AM⊥PC. ……1分
19.解:∵圆C经过点A(2 , 0) 和点A?,又点A(2 ,
0)和点A?关于直线.files/image317.gif) 对称,
对称,
∴由垂径定理,可知直线.files/image317.gif) 必过圆C的圆心。
……1分
必过圆C的圆心。
……1分
联立方程,可得.files/image303.gif)
.files/image334.gif) 解得
解得.files/image336.gif) 或
或.files/image338.gif) ……2分
……2分
∵.files/image340.gif) >0,∴所求的圆的方程为
>0,∴所求的圆的方程为.files/image342.gif) ……1分
……1分
∵过点B.files/image344.gif) 的直线
的直线.files/image320.gif) 与该圆相切,易知B
与该圆相切,易知B.files/image344.gif) 在圆外。 ……1分
在圆外。 ……1分
∴过点B.files/image344.gif) 与该圆相切的切线一定有两条。
……1分
与该圆相切的切线一定有两条。
……1分
不妨设直线.files/image320.gif) 的方程为
的方程为.files/image348.gif) ……1分
……1分
则有.files/image303.gif)
.files/image350.gif) =2
……2分
=2
……2分
解之,得.files/image352.gif) .
……1分
.
……1分
易知另一条切线的方程.files/image354.gif) ……1分
……1分
∴所求的直线方程为.files/image356.gif) 或
或.files/image354.gif) ……1分
……1分
.files/image359.jpg)
.files/image361.jpg) 20.(Ⅰ)
20.(Ⅰ)
.files/image362.gif)
.files/image364.jpg)
21.(文)解:(Ⅰ)由题意,知双曲线.files/image366.gif) 的右准线方程为
的右准线方程为.files/image368.gif) ……1分
……1分
经过第一象限的双曲线的渐近线的方程为.files/image370.gif) ……1分
……1分
联立.files/image372.gif) 可得点
可得点.files/image374.gif) ……1分
……1分
.files/image376.jpg)
(Ⅱ)由(Ⅰ),可知点P的坐标为.files/image378.gif) 双曲线的焦点的坐标为
双曲线的焦点的坐标为.files/image380.gif) .
.
……1分
而.files/image380.gif) 也是抛物线
也是抛物线.files/image383.gif) 的焦点,设PF所在的直线方程为
的焦点,设PF所在的直线方程为
.files/image385.gif) ,与抛物线相交于
,与抛物线相交于.files/image387.gif) 、
、.files/image389.gif) 两点。 ……1分
两点。 ……1分
联立.files/image391.gif) 可得
可得.files/image393.gif) ……1分
……1分
其两根.files/image395.gif) 、
、.files/image397.gif) 分别是A、B的横坐标,∴
分别是A、B的横坐标,∴.files/image399.gif) ……1分
……1分
∴有抛物线的焦点弦长公式,可知.files/image401.gif) ……1分
……1分
.files/image403.jpg) ∴直线PF被抛物线截得的线段长为
∴直线PF被抛物线截得的线段长为.files/image405.gif) ……1分
……1分
.files/image407.jpg)
.files/image409.jpg)
.files/image411.jpg)
.files/image413.jpg)
.files/image415.jpg)
.files/image417.jpg)
.files/image419.jpg)
.files/image421.jpg)
.files/image423.jpg)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com