
题目列表(包括答案和解析)
(1)先化简,再求值: (1)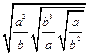 ,其中
,其中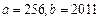 ;
;
(2)化简: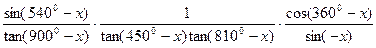
一个口袋里有带标号的7个白球、3个黑球,事件A:从袋中摸出1个放回再摸出1个,两次摸出的是1白1黑的概率为________
(05年湖北卷)(12分)
设A、B是椭圆![]() 上的两点,点N(1,3)是线段AB的中点,线段AB的垂直平分线与椭圆相交于C、D两点.
上的两点,点N(1,3)是线段AB的中点,线段AB的垂直平分线与椭圆相交于C、D两点.
(Ⅰ)确定![]() 的取值范围,并求直线AB的方程;
的取值范围,并求直线AB的方程;
(Ⅱ)试判断是否存在这样的![]() ,使得A、B、C、D四点在同一个圆上?并说明理由.
,使得A、B、C、D四点在同一个圆上?并说明理由.
(此题不要求在答题卡上画图)
(05年湖北卷文)(12分)
某会议室用5盏灯照明,每盏灯各使用灯泡一只,且型号相同.假定每盏灯能否正常照明只与灯泡的寿命有关,该型号的灯泡寿命为1年以上的概率为p1,寿命为2年以上的概率为p2.从使用之日起每满1年进行一次灯泡更换工作,只更换已坏的灯泡,平时不换.
(Ⅰ)在第一次灯泡更换工作中,求不需要换灯泡的概率和更换2只灯泡的概率;
(Ⅱ)在第二次灯泡更换工作中,对其中的某一盏灯来说,求该盏灯需要更换灯泡的概率;
(Ⅲ)当p1=0.8,p2=0.3时,求在第二次灯泡更换工作,至少需要更换4只灯泡的概率(结果保留两个有效数字).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com